资金的等值计算
资金的时间价值
不同时间发生的等额资金在价值上的差别称为资金的时间价值
也即资金在生产和流通过程中随着时间推移而产生的增值
时间价值的表现形式:
- 利润/收益 Income/profit:资金投入生产或流通领域产生的增值
- 利息 Interset:资金存入银行或向银行贷款所得到或付出的增值额
时间价值的衡量尺度:
- 绝对尺度:利息或收益
- 相对尺度:利息率或收益率
利息:贷款人向借款人让渡资金使用权而得到的一种报酬
利率:一个计息周期内,利息总额与本金的比率
单利
以借款本金为计息基数,利息不再生息
复利
以本金与累计利息之和为计息基数
技术经济分析中时间价值一般采用复利法,充分反映资金的时间价值
不同计息周期的利率换算
(以年利率举例)
名义利率 r、计息周期 m、每一周期的计息利率 r/m
实际 (有效) 利率 i
一年内获得的利息与年初本金之比计算的年利率
月利率 1%
名义利率 12%
实际利率
如果一年计息 m 次
资金等值
通过等值计算,可以把不同时间点发生的资金金额换算到同一时间点进行价值比较
等值资金
在利率一定的条件下,
不同时间上绝对数额不等,
而经济价值相等的若干资金
折现 Discount
把将来某一时间点上的资金值换算到现在时间点上的等值资金值
不一定是折现到期初,只是一个相对的概念,只要将之后时间点转换到前面的时间点就算是折现
折现率 Discount Rate i
资金等值计算中使用的反映资金时间价值的参数
现值 Present Value P
相对的概念,任意时刻都可作为现值
终值 Future Value F
与现值等价的在将来某时点的资金值
等年值/年金 Annual Value A
分期等额收支的资金值
n 年标准形式:
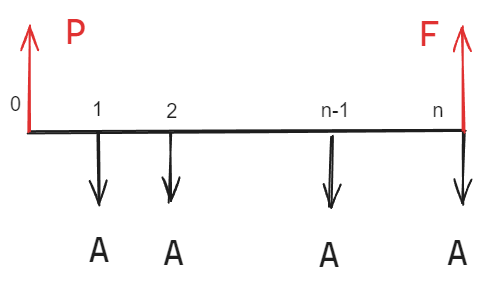
一次收付
一次收付型:
分析系统的现金流量时,无论流入还是流出,
均在一个时间点 一次发生
等额分付
多次支付
现金流入和现金流出在多个时间点上
等额分付
多次支付的一种形式
等额系列现金流
现金流序列连续,且数额相等
等比数列求和
(n 年年末)
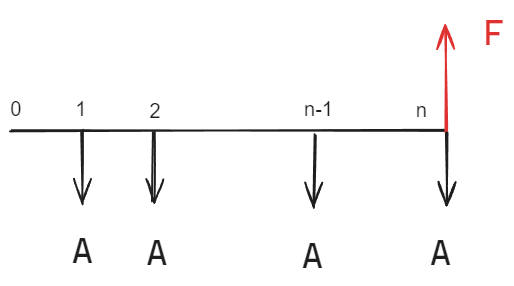
(n 年年初)
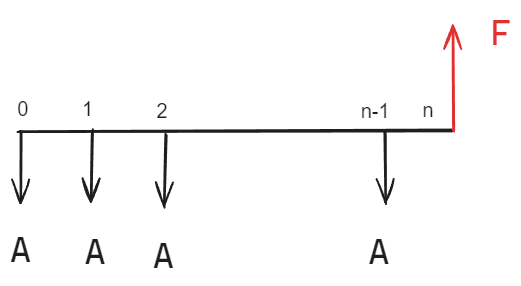
**
收付年金终值的逆运算
(n 年年末)
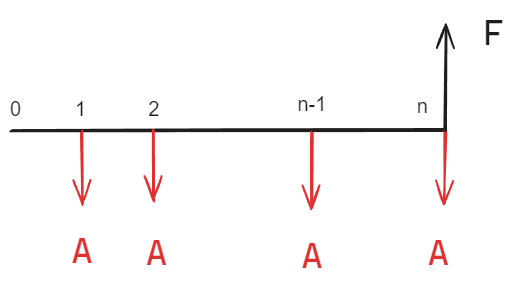
(n 年年末)
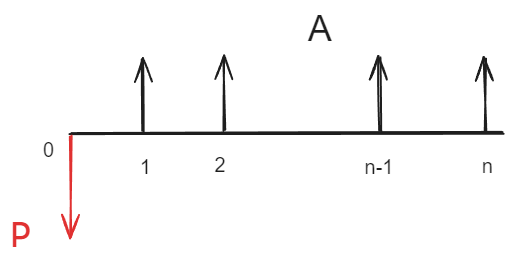
年金现值的逆运算
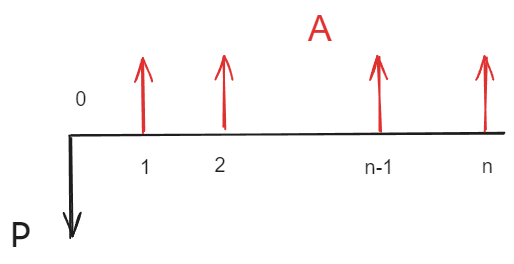
偿还贷款
graph LR
偿还贷款 --> 等额利息 & 等额本金 & 等额本息 & 一次支付
等额本金:每年年末偿还固定的本金以及所欠利息
等额本息:每年年末等额偿还
等额利息 :每年年末只偿还利息,最后一年年末还清本金
一次支付 :最后一年年末一次偿还本息