微分中值定理
Mean Value Theorem for Derivatives
建立了导数和函数之间的关系
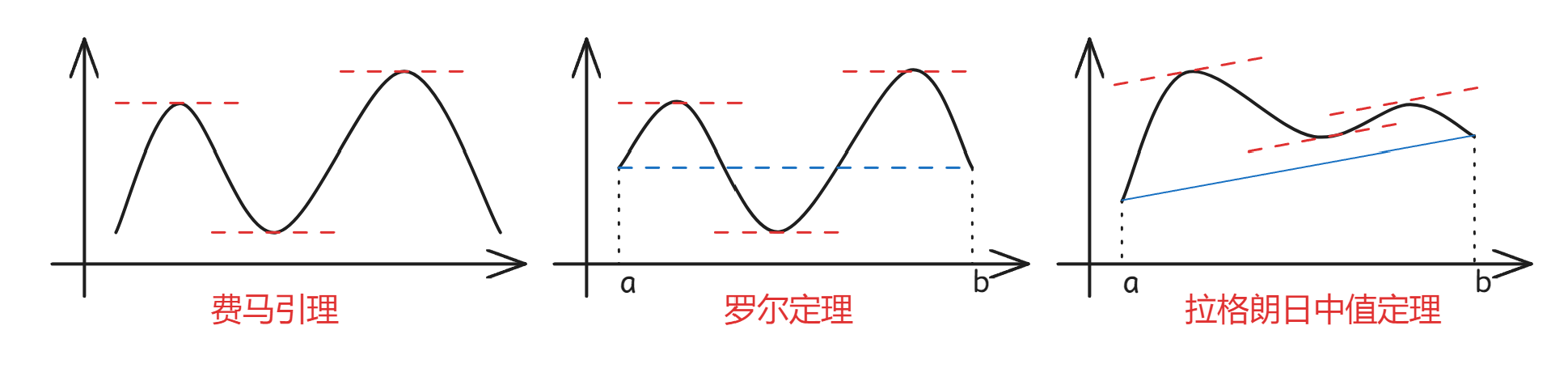
费马引理 Fermat
函数
如果对任意的
通常称导数为 0 的点为 驻点/稳定点/临界点
一、罗尔定理 Rolle
直观理解:如果区间端点的函数值相等,则在区间内部必定可以找到斜率为零的点
如果函数
- 在闭区间
上 连续 - 在开区间
上 可导* - 在区间端点处的函数值相等
那么在 内至少有一点 ,使得
二、拉格朗日中值定理 Lagrange
直观理解:罗尔定理的一般化,几何意义就是区间内存在一点的切线斜率等于区间端点连线的斜率。
如果函数
- 在闭区间
上 连续 - 在开区间
上 可导*
那么在 内至少有一点 , 使得等式成立:
微分中值定理/有限增量定理: 在区间
实际上,从数值计算方法的角度看,也是龙格-库塔法的核心思想之一
三、柯西中值定理 Cauchy
如果函数
- 在闭区间
上 连续 - 在开区间
上 可导* - 对任一
,
那么在 内至少有一点 , 使得:
微分中值定理的实际应用
构造辅助函数,基本思路都是构造辅助函数,满足所需的条件