异步电机线性化动态建模
系统组成
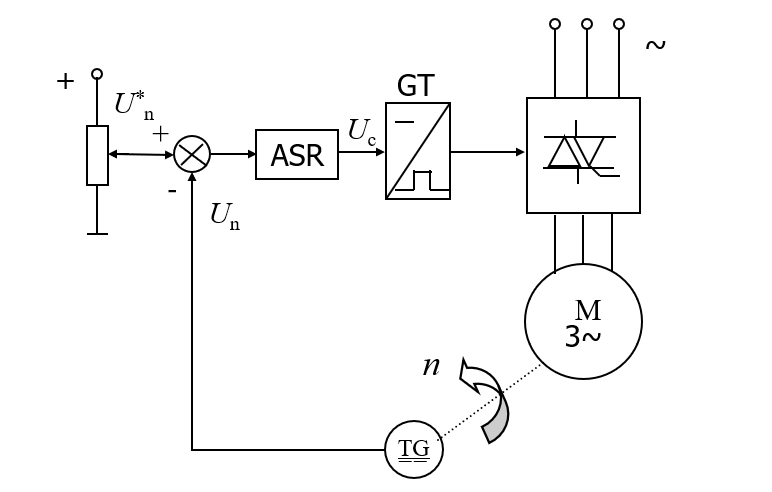
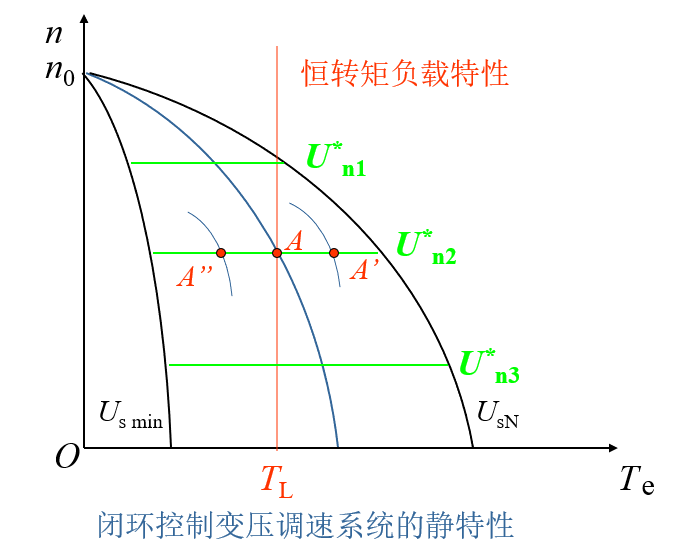
系统的静特性
当转速或转差率一定时,
电磁转矩与定子电压的平方成正比
系统带负载在 A 点运行时,
- 如果负载增大
引起转速下降,反馈控制作用能提高定子电压,
从而在右边一条机械特性上找到新的工作点 A’ - 当负载降低时
会在左边一条特性上得到定子电压低一些的工作点 A’’
A’’、A、A’连接起来便是闭环系统的静特性
在不同电压的开环机械特性上各取一个相应的工作点,连接起来便得到闭环系统静特性
不同于直流电机闭环变压调速系统的地方是:
静特性左右两边都有极限,不能无限延长,它们是额定电压
当负载变化时,如果电压调节到极限值,闭环系统便失去控制能力,系统的工作点只能沿着极限开环特性变化
结构框图
静态结构框图
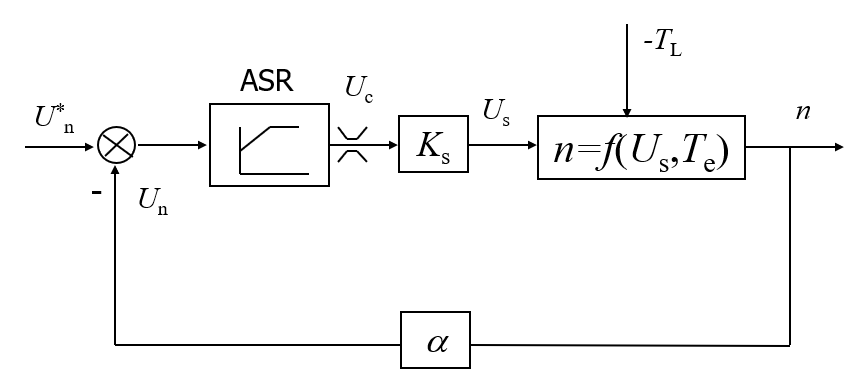
动态结构框图
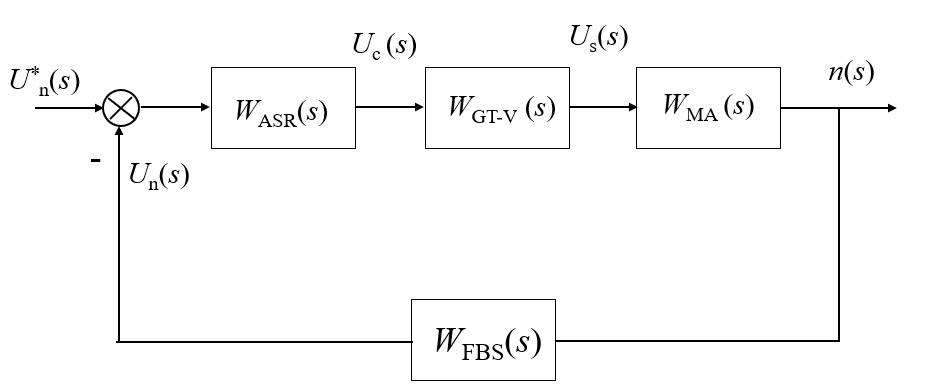
各环节的传递函数
转速调节器ASR
PI调节器,以消除静差并改善动态性能
电力电子变换器 GT-V
三相触发脉冲作用于晶闸管门极端
模拟信号转化为触发脉冲
测速反馈环节FBS
考虑到反馈滤波作用
低通滤波,滤除高次谐波
转折频率
对高频信号滤波,
异步电机近似的传递函数
稳态工作点附近的偏微线性化,近似求取
当s 很小时: 近似的线性机械特性
设 A 为近似线性机械特性上的一个稳态工作点
同步角转速 定子角转速
运动方程:
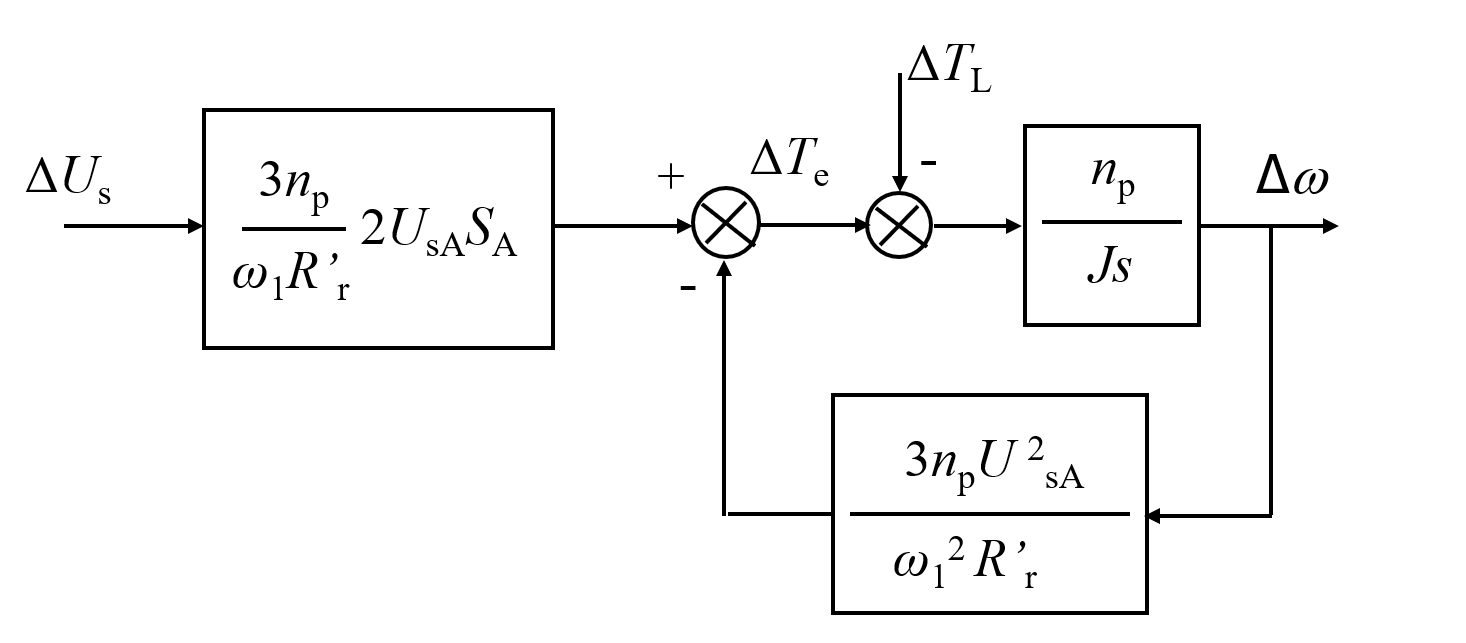
异步电机的传递系数
机电时间常数
基本流程
给出电机的机械特性方程
在线性段范围内,简化方程
找典型工作点
增量
写出微偏表达式
相减得到纯
将
明确传递函数的输入
缺少运动方程,写出运动方程
画出结构框图
非线性环节的线性化
找经典工作点,偏微线性化
不同传递函数代表不同的工况(工作状态)
工作负荷、原料属性
时间常数变大,PID 调节器应该增大比例 P,积分作用减小(来减小偏差)
现场调三个参数的经验
电磁惯性
电压到电流的过程
模型的误差可以被反馈抑制,
虽然有很大的近似性,但是误差仍然小到可以用来分析问题