直流电机反馈控制的动态建模
动态建模的步骤
- 根据系统中各环节的物理规律,
列出描述该环节动态过程的微分方程; - 求出各环节的传递函数;
- 组成系统的动态结构图并求出系统的传递函数
转速负反馈的原理图:
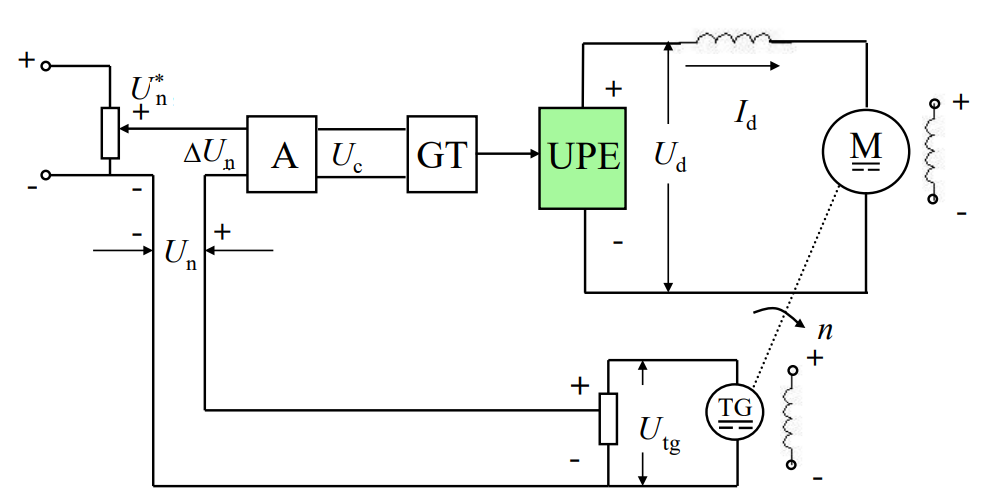
闭环调速系统的稳态结构框图:
关键就是
- 对各个环节进行动态建模列写传递函数
- 知道了各环节的传递函数后,把它们按在系统中的相互关系组合起来,就可以画出闭环直流调速系统的动态结构图
- 将静态的系统结构图画为动态结构图
电力电子变换器的动态建模
不同电力电子变换器的传递函数,表达式基本一致
都为纯滞后环节 (见: V-M系统晶闸管整流)
控制与检测环节的动态建模
比例放大器和测速反馈环节:它们的响应都可以认为是瞬时的,因此它们的传递函数就是它们的放大系数
电机的动态建模
调压调速
输入是调压调速的电压
输出是电机的实际转速
对电机的建模: 四个方程
电机的三个方程+电动势方程
直流电机等效电路:
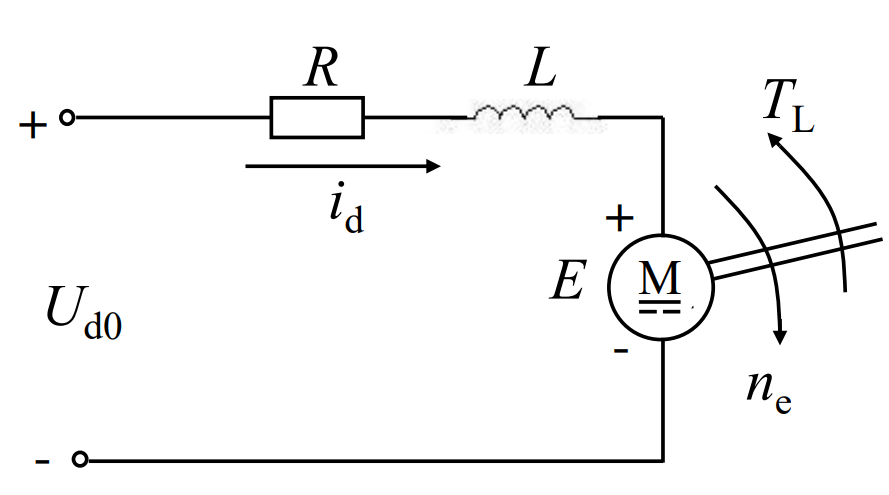
列写方程
- 电路方程:
- 反电动势方程:
反电动势是电机在旋转时切割磁力线产生的电压
在直流电机中,反电动势与电机的转速成正比
电机产生的反电动势 电机的反电动势常数
- 电磁转矩方程:
电机产生的实际的电磁转矩 电机需要克服的外部负载的转矩 电机额定励磁下的转矩系数 流过电机电枢(定子)的电流 负载电流(Load Current)
即为了克服负载所需的电枢电流
- 动力学方程:
电力拖动系统折算到电机轴上的飞轮惯量
写传递函数
- 电磁时间常数
- 机电时间常数
结构框图
由上面两个式子得到:
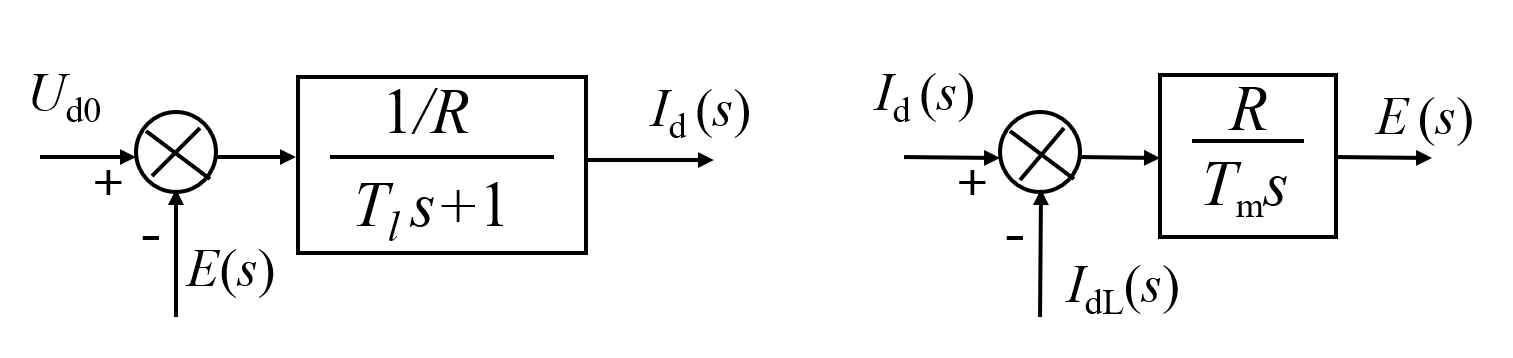
最终得到整个直流电机的动态结构图:
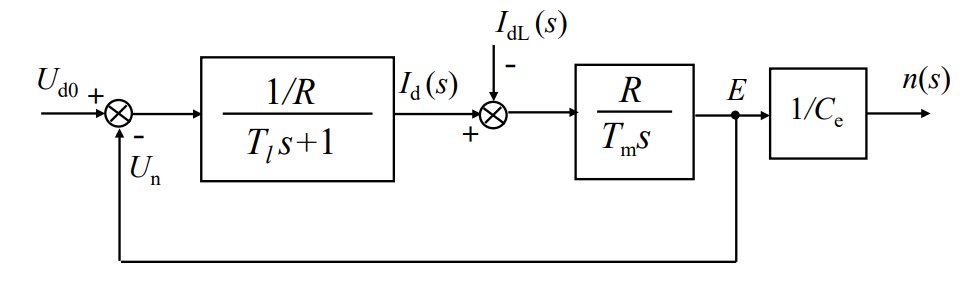
经过框图变换得到:
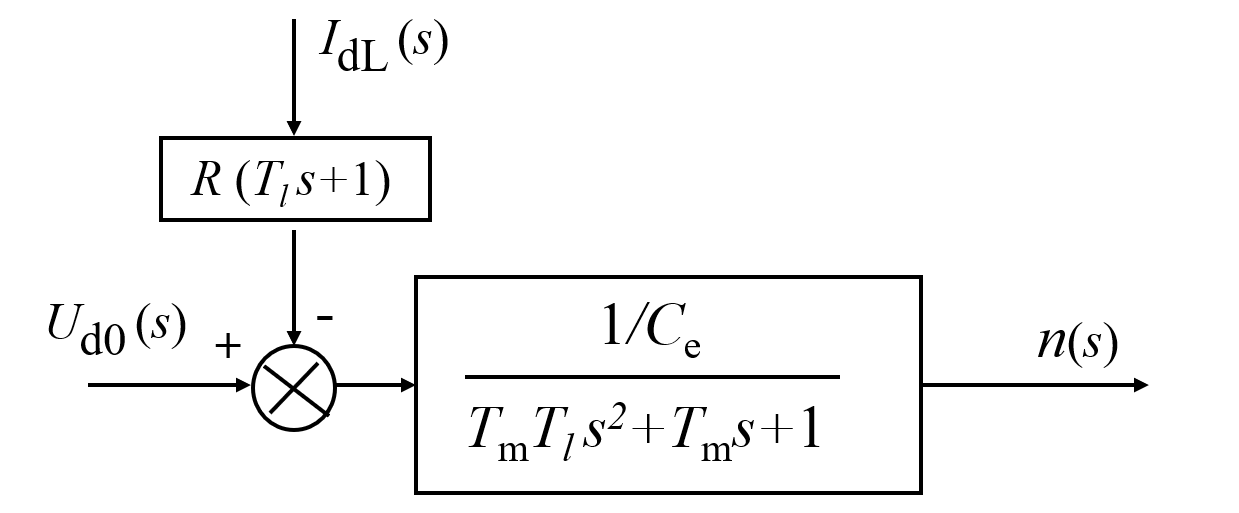
机电时间常数大于电磁时间常数
功率器件的时间常数
动态结构框图
将上面得到的各个部分的传递函数组合到一起,得到最终整个直流调速系统的动态结构框图
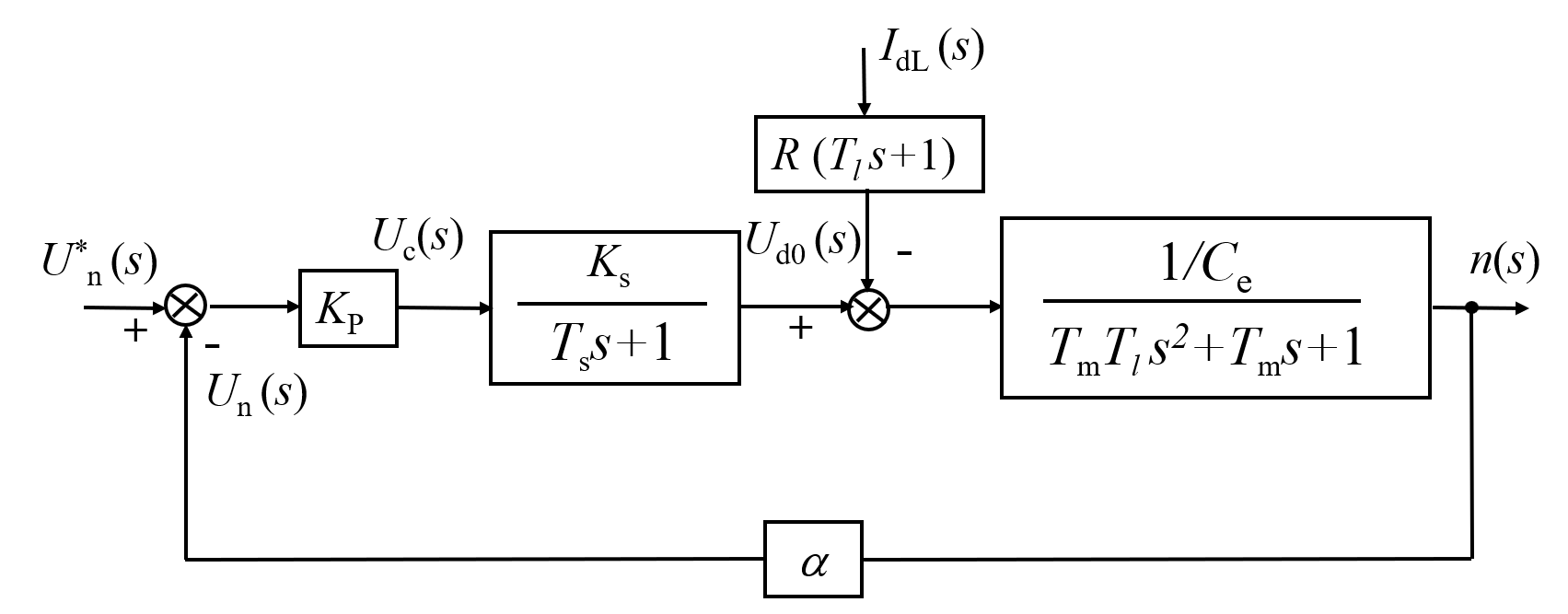
动态框图:负载(转矩电流)为干扰
稳态框图:电枢电流为干扰
传递函数
由动态结构框图得到传递函数:
开环传递函数:
闭环传递函数: