Transfer Function Matrix
传递函数的矩阵形式,用来研究多输入-多输出系统,实际上反映了系统中能控且能观的子系统的动力学行为
一、传递函数矩阵基本概念
传递函数矩阵:初始条件为零时,输出向量的拉普拉斯变换与输入向量的拉普拉斯变换式之间的传递关系。(类似与传递函数的定义)
系统状态空间方程为:
初始条件为零时,拉普拉斯变换为:
进一步整理得到:
最终得到系统的传递矩阵表达式为:
计算传递函数矩阵要正确计算矩阵的逆,由于存在 ,只能使用伴随矩阵法求逆。
二、子系统连接的传递函数矩阵
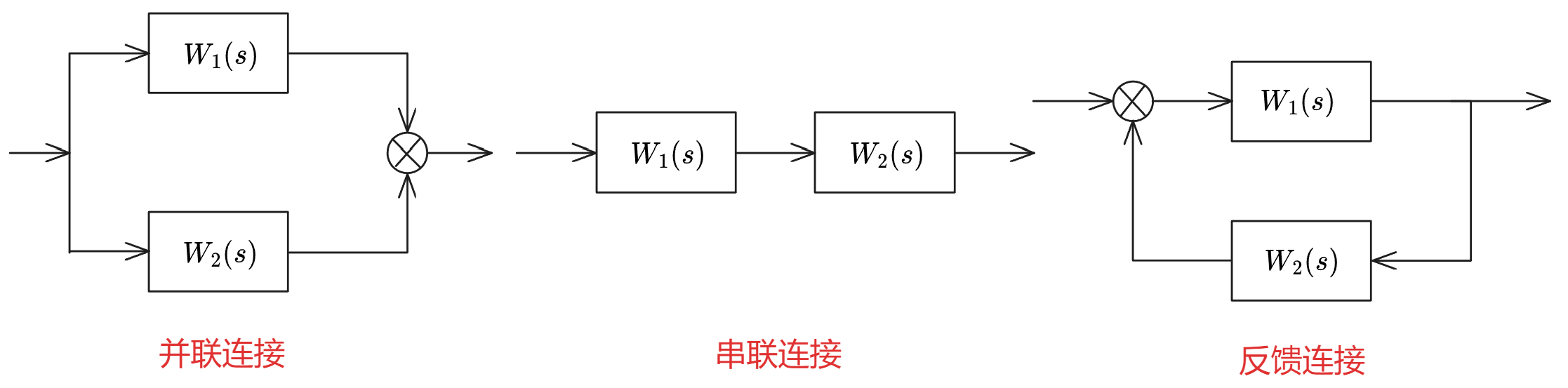
1. 并联连接
子系统并联时,系统传递函数阵等于子系统传递函数阵的代数和
2. 串联连接
子系统串联时,系统传递函数阵等于子系统传递函数阵之积(注意矩阵相乘的先后次序不能改变)
3. 反馈连接
也要注意矩阵乘法不满足交换律,注意乘的次序
实际例题
计算传递函数:
求闭环传递函数矩阵
