根轨迹法

(terminology:：Root Locus Method)
根轨迹/根迹：
开环传函某一参数从零变到无穷时，闭环系统特征方程的根在s 平面上变化的轨迹

\begin{aligned} G (s) & = \frac{b_{0} (s - z_{1}) (s - z_{2}) \dots (s - z_{m})}{a_{0} (s - p_{1}) (s - p_{2}) \dots (s - p_{n})} = K^{*} \frac{\prod_{i = 1}^{m} (s - z_{i})}{\prod_{j = 1}^{n} (s - p_{j})} \end{aligned}

\begin{aligned} G (s) = K_{G}^{*} \frac{\prod_{i = 1}^{f} (s - z_{i})}{\prod_{i = 1}^{q} (s - p_{i})} \\ H (s) = K_{H}^{*} \frac{\prod_{j = 1}^{l} (s - z_{j})}{\prod_{j = 1}^{h} (s - p_{j})} \\ G (s) H (s) = K_{G}^{*} K_{H}^{*} \frac{\prod_{i = 1}^{f} (s - z_{i})}{\prod_{i = 1}^{q} (s - p_{i})} \frac{\prod_{j = 1}^{l} (s - z_{j})}{\prod_{j = 1}^{h} (s - p_{j})} \end{aligned}

\begin{aligned} Φ (s) = K_{G}^{*} (s) \frac{\prod_{i = 1}^{f} (s - z_{i}) \prod_{j = 1}^{h} (s - p_{j})}{\prod_{i = 1}^{n} (s - p_{i}) + K^{*} \prod_{j = 1}^{m} (s - z_{j})} \\ f + l = m q + h = n \end{aligned}

根轨迹法的基本任务：

由已知的开环零、极点的分布及根轨迹增益，通过图解的方法找出闭环极点
（确定闭环极点后，确定闭环传递函数的形式。在已知闭环传递函数时，利用拉普拉斯逆变换求出闭环系统的时间响应）

闭环特征方程： $1 + G (s) H (s) = 0$
根轨迹方程： $G (s) H (s) = - 1$

\begin{array}{r} K^{*} \frac{\prod_{j = 1}^{m} (s - z_{j})}{\prod_{i = 1}^{n} (s - p_{i})} = - 1 \end{array}

\begin{aligned} \sum_{j = 1}^{m} ∠ (s - z_{j}) - \sum_{i = 1}^{n} ∠ (s - p_{i}) = (2 k + 1) π \end{aligned}

确定s平面上根轨迹的充分必要条件
根轨迹上的点满足相角条件，为闭环传函的极点

\begin{aligned} K^{*} = \frac{\prod_{i = 1}^{n} | s - p_{i} |}{\prod_{j = 1}^{m} | s - z_{j} |} \end{aligned}

确定s平面上各点的 $K^{*}$ 值时使用

分析系统的性能

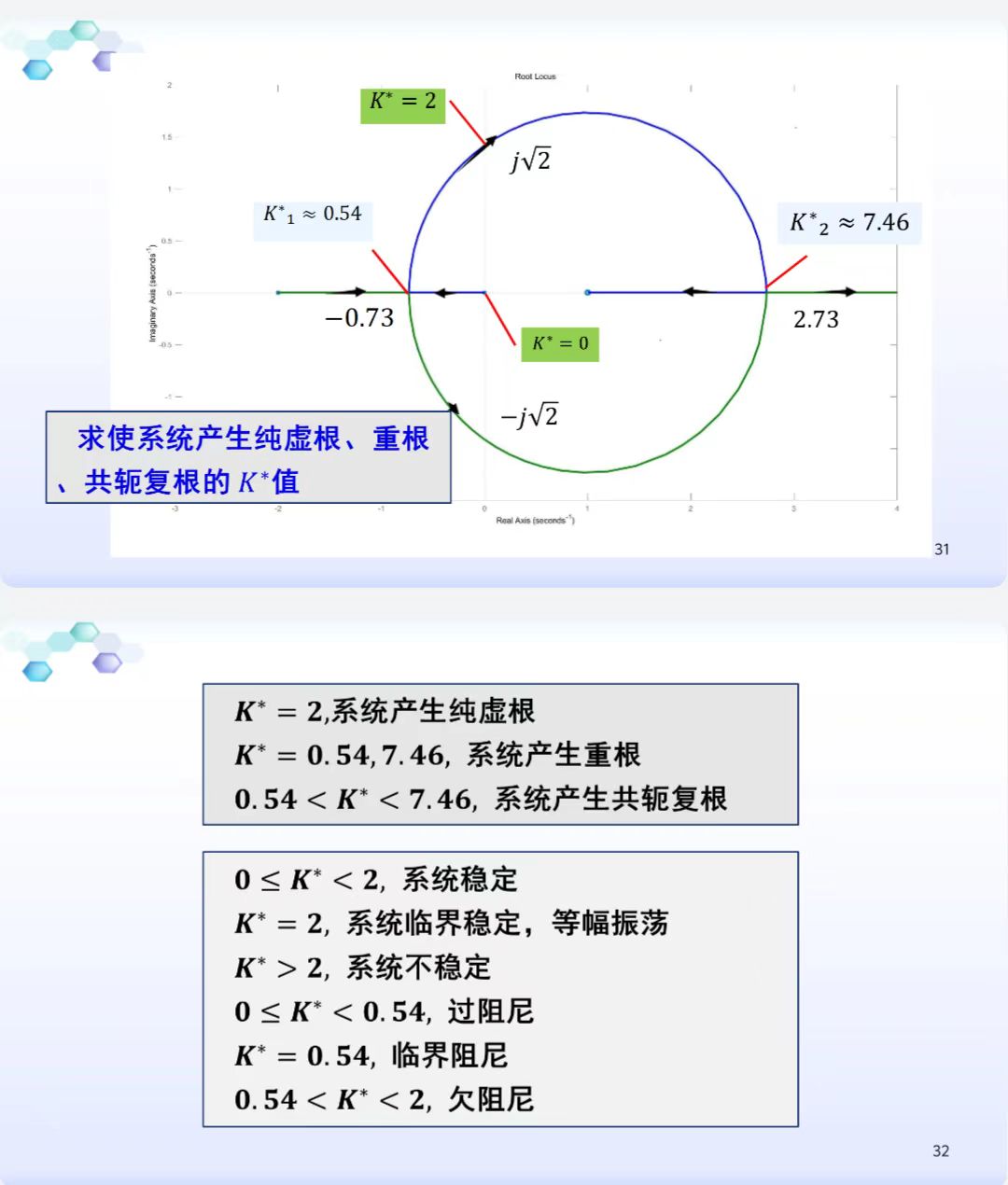
直接观察根轨迹判断系统的稳定性及性能指标:

当闭环特征根位于 s 平面的右半平面时，闭环系统不稳定 发散特性
当闭环特征根位于 s 平面的虚轴上时，闭环系统临界稳定 等幅振荡
当闭环特征根位于 s 平面的左半平面时，闭环系统稳定
- 左半实轴上时，系统输出的相应模态表现为惯性特性
- 非实轴区域时，系统输出的相应模态表现为衰减振荡特性

零极点分析
引入开环零点改善系统动态特性
使用主导极点对高阶系统降阶

在开环系统中增加负实部零点，可以使根轨迹向左方移动，
所引入的零点越靠近虚轴，根轨迹向左方移动的越显著，从而增加系统的相对稳定性

计算根轨迹上特殊位置的点及对应的 $K^{*}$ ，分析系统动态响应
分析根轨迹与指定阻尼线相交的闭环极点（极点配置），近似估算系统的动态性能