State Space Representation
得到状态空间表达式
一、从内部结构机理建立
1.1 系统模拟结构图建立
和经典控制理论的系统结构框图一致,使用框图表示信号传递关系。
积分器的个数和状态变量数一致,积分器的输出就为状态变量。输入 , 输出
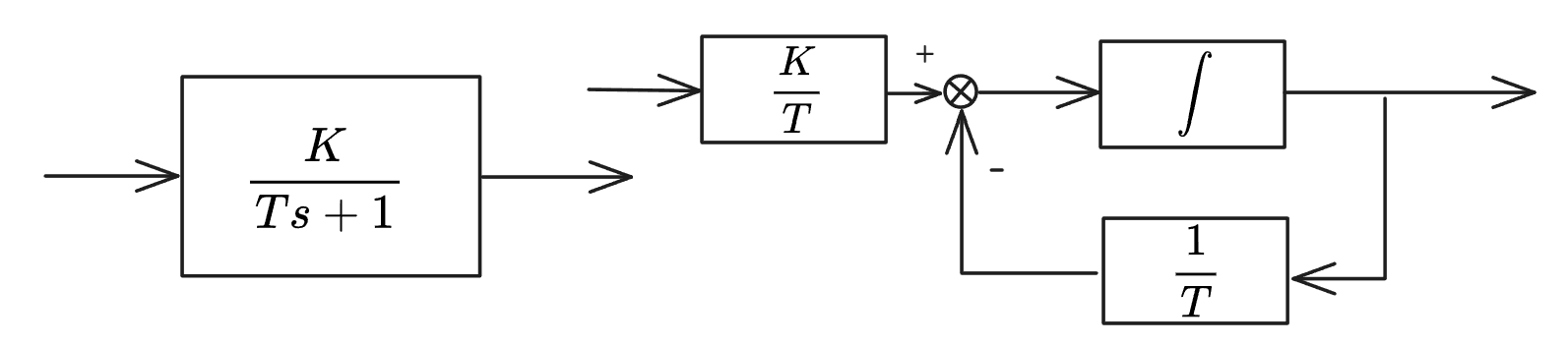
1.2 系统机理建立
二、从外部描述建立
实现问题:由描述系统输入-输出动态关系的微分方程/差分方程或传递函数建立系统的状态空间表达式。(保持了原有的输入-输出关系,又将系统的内部关系揭示出来;注意系统的实现是不唯一的)
2.1 传递函数无零点
高阶微分方程:
对应传递函数:
取系统状态空间表达式为:
对应状态空间表达式:
系统矩阵为特征多项式对应的友矩阵!
2.2 传递函数有零点
高阶微分方程:
对应传递函数:
对应状态空间表达式:(以下是当 时情况,如果 ,注意 即可)
形式一:
(实际上为状态空间表达式的能控标准型和能观标准型#1.1 能控标准 I 型)
形式二:
