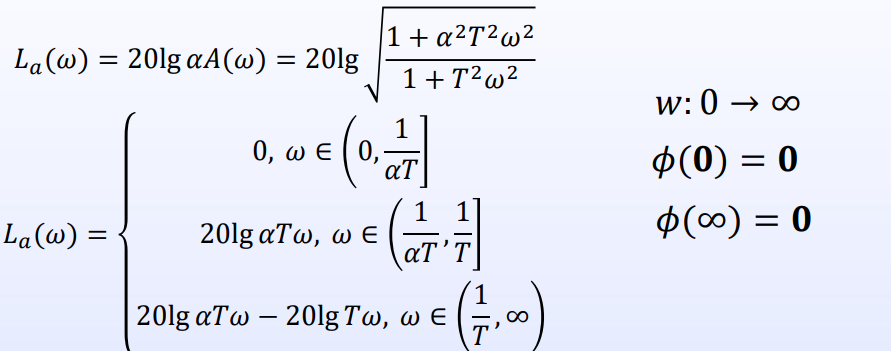系统稳定性和动态性能
为了补偿增益的衰减,需要串联一个比例放大环节 / 放大器增益需要提高 倍
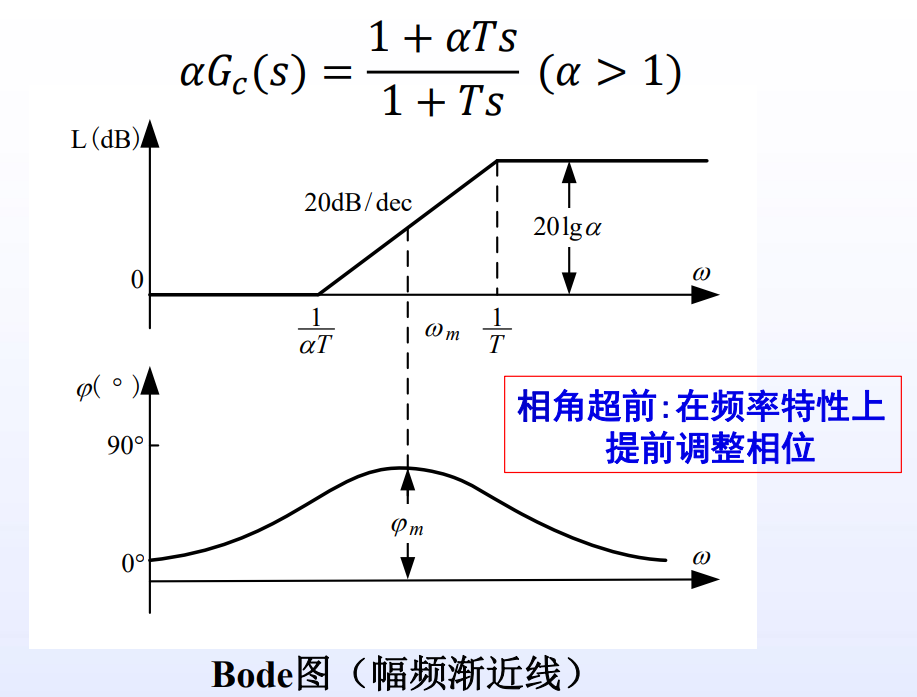
相关参数
分度系数:
时间常数:
转折频率:
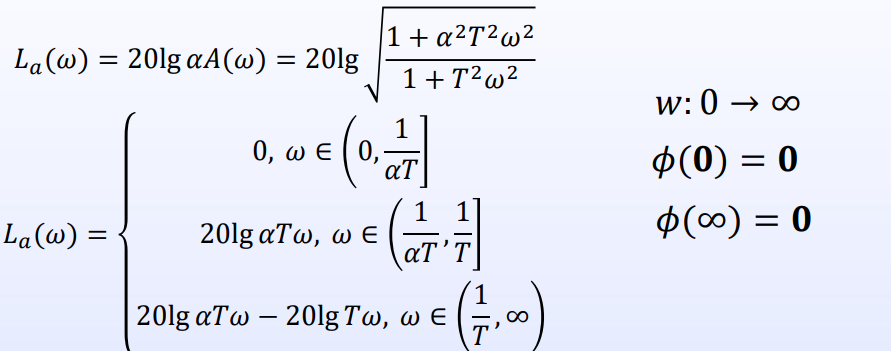
最大超前角频率:
最大超前角:
对数幅频值:
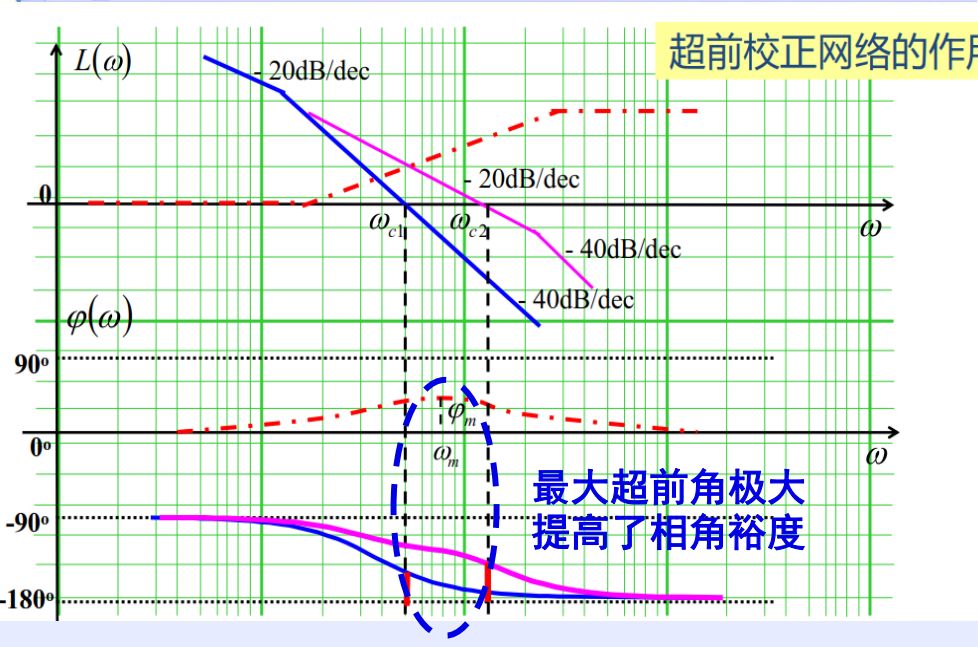
对系统的影响
- 提高稳定裕度:相角裕度变大,稳定性增强
- 改善动态性能:截止频率 变大,带宽频率 变大,响应时间减小
- 抗中高频干扰能力减弱:中高段,降低抗干扰能力
设计校正的步骤
-
根据稳态要求,确定未校正系统的放大系数
-
画出未校正系统 的Bode图 (渐近特性图)
求未校正系统的截止频率 与相角裕度
注意是要求渐近特性
这里真正需要求的其实是在期望截止频率处的幅值,之后利用此数值作为超前校正拉高的值
-
根据期望的截止频率计算出超前校正的相关参数
最大超前角频率 = 期望的系统截止频率
来计算相关参数:
期望的截止频率满足此关系
先计算未校正系统在期望截止频率处的对数幅值
此幅值作为校正环节 “抬高”的幅值
(本质上就是在此点处将幅值拉高,使之作为截止频率)
得到参数
-
超前校正环节
为了补偿无源超前网络产生的增益衰减,放大器增益需提高 倍
-
验证校正后系统的性能指标
校正后的系统