机器学习实践
一、数据集
数据集划分
- 训练集 Training Set:训练模型,通过训练集的数据让我们确定拟合曲线的参数。
- 验证集 Validation Set:也叫做开发集Dev Set,用来做模型选择model selection,即做模型的最终优化及确定的,用来辅助模型的构建,即训练超参数,可选。
- 测试集 Test Set: 为了测试已经训练好的模型的精确度。
机器学习:60%,20%,20%;70%,10%,20%
深度学习:98%,1%,1% (假设百万条数据)
交叉验证
- 使用训练集训练出k个模型
- 用k个模型分别对交叉验证集计算得出交叉验证误差(代价函数的值)
- 选取代价函数值最小的模型
- 用步骤3中选出的模型对测试集计算得出推广误差
不平衡数据的处理
数据不平衡:指数据集中各类样本数量不均衡的情况。常用不平衡处理方法有采样和代价敏感学习。
采样:欠采样、过采样和综合采样
- SMOTE 算法(过采样):合成新的少数类样本,而不是简单地复制样本。Synthetic Minority Over-sampling Technique
- 代价敏感学习:为不同类别的样本提供不同的权重。为少类样本设置更高的学习权重,提高对少类样本分类的查全率,但是也会将很多多类样本分类为少类样本,降低少类样本分类的查准率。
二、评价指标
混淆矩阵(confusion_matrix):
| 实际 \ 预测 | Positive | Negative |
|---|---|---|
| Positive | TP | FN |
| Negative | FP | TN |
正确肯定 TP: 预测为真,实际为真 (True Positive)
正确否定 TN:预测为假,实际为假 (True Negative)
错误肯定 FP: 预测为真,实际为假 (False Positive)
错误否定 FN: 预测为假,实际为真(False Negative)
- 正确率:
- 精度:
- 召回率:
- F1:

三、过拟合与欠拟合
数据量达到一定级数后 ,都有相近的高准确度
3.1 处理过拟合
- 获得更多的训练数据:解决过拟合问题最有效的手段,因为更多的样本能够让模型学习到更多更有效的特征,减小噪声的影响。
- 降维:丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征,或者使用一些模型选择的算法来帮忙(例如PCA)。
- 正则化:regularization,保留所有的特征,但是减少参数的大小(magnitude) ,它可以改善或者减少过拟合问题。
- 集成学习方法:集成学习是把多个模型集成在一起,来降低单一模型的过拟合风险
3.2 处理欠拟合
- 添加新特征:当特征不足或者现有特征与样本标签的相关性不强时,模型容易出现欠拟合。通过挖掘组合特征等新的特征,往往能够取得更好的效果。
- 增加模型复杂度:简单模型的学习能力较差,通过增加模型的复杂度可以使模型拥有更强的拟合能力。例如,在线性模型中添加高次项,在神经网络模型中增加网络层数或神经元个数等。
- 减小正则化系数:正则化是用来防止过拟合的,但当模型出现欠拟合现象时,则需要有针对性地减小正则化系数。
四、归一化/标准化
提升模型精度:不同维度之间的特征在数值上有一定比较性,可以大大提高分类器的准确性。
加速模型收敛:最优解的寻优过程明显会变得平缓,更容易正确的收敛到最优解。
-
归一化:将数据映射到
,使得各特征对目标变量的影响一致,会改变特征数据分布。 -
标准化:Z-Score标准化,处理后的数据均值为0,方差为1。为了不同特征之间具备可比性,数据分布没有发生改变。(当数据特征取值范围或单位差异较大时,最好是做一下标准化处理)
线性模型,如基于距离度量的模型包括KNN(K近邻)、K-means聚类、感知机和SVM。线性回归类的几个模型一般情况下也是需要做数据归一化/标准化处理的。
决策树、基于决策树的Boosting和Bagging等集成学习模型对于特征取值大小并不敏感,如随机森林、XGBoost、LightGBM等树模型,以及朴素贝叶斯,以上这些模型一般不需要做数据归一化/标准化处理。
五、正则化
L1 正则化( Lasso回归)
可以产生稀疏模型:在损失函数中加入权值向量w的绝对值之和,使权重稀疏。使解更加靠近某些轴,而其它的轴则为0,所以能使得到的参数稀疏化
L2 正则化( 岭回归)
可以防止过拟合:在损失函数中加入权值向量w的平方和,使权重平滑。使解更加靠近原点,能降低参数范数的总和。
弹性网络 Elastic Net
Dropout正则化
类似于𝐿2正则化,但是被应用的方式不同,dropout也会有所不同,甚至更适用于不同的输入范围(在训练阶段使用,在测试阶段不使用)
- keep-prob=1 (没有 dropout)
- keep-prob=0.5 (常用取值,保留一半神经元)
Early stopping
提早停止训练神经网络 ,只运行一次梯度下降,可以找出𝑤的较小值,而无需尝试很多值。
计算机视觉:数据增强
随意翻转、镜像;随意裁剪;扭曲变形图片;颜色转换;R、G和B三个通道上加上不同的失真值,产生大量的样本
六、偏差和方差
方差Variance:预测值的变化范围,离散程度,也就是离其期望值的距离。方差越大,数据的分布越分散
偏差Bias: 预测值(估计值)的期望与真实值之间的差距,偏差越大,越偏离真实数据。
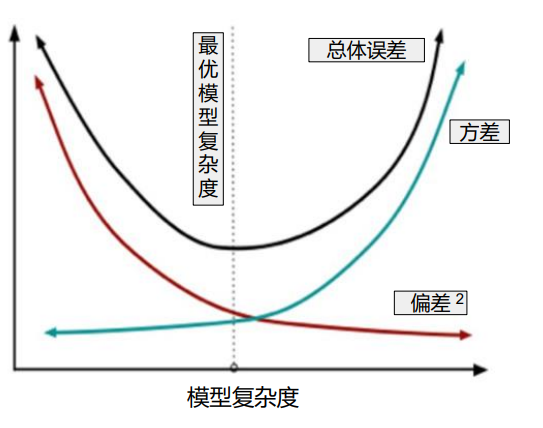
随着模型复杂度的增加,方差会逐渐增大,偏差会逐渐减小。
训练集误差和交叉验证集误差近似时:偏差/欠拟合
交叉验证集误差远大于训练集误差时:方差/过拟合
- 获得更多的训练实例——解决高方差
- 尝试减少特征的数量——解决高方差
- 尝试获得更多的特征——解决高偏差
- 尝试增加多项式特征——解决高偏差
- 尝试减少正则化程度λ——解决高偏差
- 尝试增加正则化程度λ——解决高方差