降维

Dimensionality Reduction
将训练数据中的样本 (实例) 从高维空间转换到低维空间，该过程与信息论中有损压缩概念密切相关。（不存在完全无损的降维）

降维概述

维数灾难(Curse of Dimensionality)：涉及数字分析、抽样、组合、机器学习、数据挖掘和数据库等诸多领域。通常是指在涉及到向量的计算的问题中，随着维数的增加，计算量呈指数倍增长的一种现象。维度太大也会导致机器学习性能的下降，并不是特征维度越大越好，模型的性能会随着特征的增加先上升后下降。

主要作用

1. 减少冗余特征，降低数据维度 （去掉冗余特征对机器学习的计算结果不会有影响）
2. 数据可视化。（t-SNE：将数据点之间的相似度转换为概率。原始空间中的相似度由高斯联合概率表示，嵌入空间的相似度由“t分布”表示，关注数据的局部结构）

• 降维的优点：减少特征的维数，减少了特征维数所需的计算训练时间；数据集特征的降维有助于快速可视化数据；通过处理多重共线性消除冗余特征。
• 降维的缺点：降维可能会丢失一些数据；主成分分析，需要考虑多少主成分是难以确定的，往往使用经验法则

奇异值分解 SVD

Singular Value Decomposition

SVD可以将一个矩阵 A 分解为三个矩阵的乘积：正交矩阵 $U,V^T$，对角矩阵 $\mathrm{\Sigma }$

$(A{A}^T)u_i={\lambda }_i{u}_i$ $U$ 矩阵中每个列向量为左奇异向量
$(A^{T}A)v_i={\lambda }_i{v}_i$ $V$ 矩阵中每个列向量为右奇异向量
${\sigma }_i=\sqrt{{\lambda }_i}$ 为奇异值，对角矩阵对角线上的奇异值递减排列

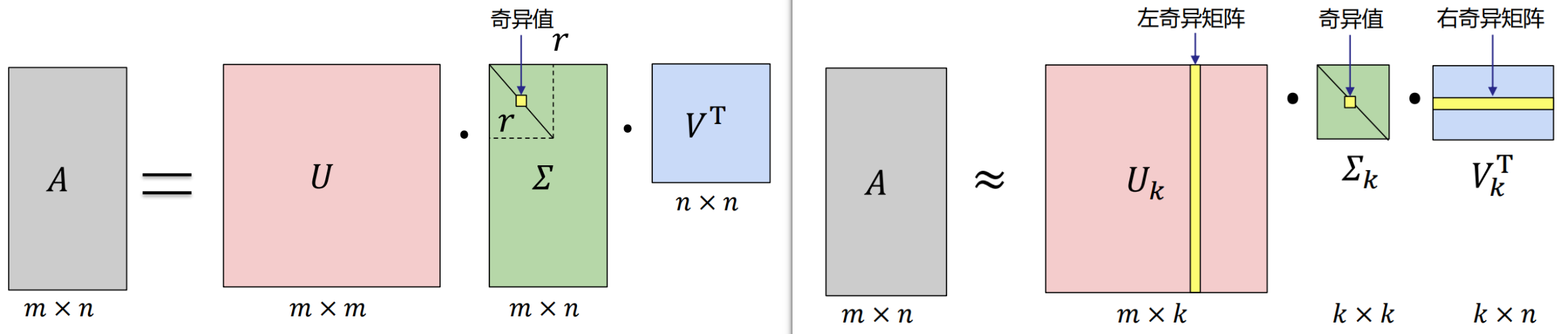
主成分分析 PCA

Principal Component Analysis
基本思想：减少数据集的特征数量，同时尽可能地保留信息：将一个大的特征集转换成一个较小的特征集，这个特征集仍然包含了原始数据中的大部分信息，从而降低了原始数据的维数。

两种实现方法

1. 基于SVD分解协方差矩阵实现PCA算法
2. 基于特征值分解协方差矩阵实现PCA算法

第一步：均值归一化，计算出所有特征的均值 $x_j=x_j-{\mu }_j$
第二步：计算协方差矩阵 $\mathrm{\Sigma }={\displaystyle \frac{1}{n}}\sum _{i=1}^n(x_i{x}_i^T)$
第三步：计算协方差矩阵的特征值和特征向量
对特征值从大到小排序，选择其中最大的 k个。然后将其对应的 k 个特征向量分别作为行向量组成特征向量矩阵 $P$

计算实例

求 $A=\left(\begin{array}{ccc}1& 2& 0\\ 2& 0& 2\end{array}\right)$ 的奇异值分解。
因为 $A$ 的秩为 2，所以最多有两个特征值，计算 $A{A}^T$ 的特征值，即可得到 $\mathrm{\Sigma }$

$A{A}^T$ 有特征值 ${\lambda }_1=9,{\lambda }_2=4$，则 $A^{T}A$ 有特征值 ${\lambda }_1=9,{\lambda }_2=4,{\lambda }_3=0$
$(\lambda I-A{A}^T)\overrightarrow{p}=\overrightarrow{0}$ 计算特征向量，作为矩阵 $U$ 的列向量
$(\lambda I-A^{T}A)\overrightarrow{p}=\overrightarrow{0}$ 计算特征向量，作为矩阵 $V$ 的列向量
（注意均将特征向量归一化为单位向量！！！）

奇异值为特征值开根号，降序排列： ${\sigma }_1=\sqrt{9}=3{\sigma }_2=\sqrt{4}=2$