模拟式PID控制器

基本概述

偏差 = 测量值 - 给定值 $ε = x_{i} - x_{S}$ ， $ε > 0$ 为正偏差， $ε < 0$ 为负偏差
输出信号变化量 $Δ y$ ， $ε > 0 \to Δ y > 0$ 为正作用控制器， $ε < 0 \to Δ y > 0$ 为负作用控制器

\begin{array}{r} W (s) = K_{p} (1 + \frac{1}{T_{i} s} + T_{d} s) \end{array}

\begin{array}{r} W (s) = K_{P} F \frac{1 + \frac{1}{F T_{I} s} + \frac{T_{D}}{F} s}{1 + \frac{1}{K_{I} T_{I} s} + \frac{T_{D}}{K_{D} s}} \end{array}

控制器之间的干扰系数： $F = 1 + α \frac{T_{D}}{T_{I}}$

一、P 运算规律

\begin{array}{r} Δ y = K_{P} ε \Rightarrow W (s) = K_{P} \end{array}

比例度 $δ$ 表示比例作用的强弱：比例度越小，比例作用越强。

\begin{array}{r} δ = \frac{\frac{ε}{ε_{m a x} - ε_{m i n}}}{\frac{Δ y}{y_{m a x} - y_{m i n}}} \times 100 % = \frac{1}{K_{P}} \times 100 % \end{array}

单独的比例作用一定会存在余差，比例作用 $K_{P}$ 越大，余差越小。（但是比例作用增大，稳定性变差，容易产生振荡）

二、PI 运算规律

积分作用可以消除余差：只要偏差存在，积分作用输出就会随时间不断变化直到偏差消除。
但是积分输出是随时间累计改变的，控制动作缓慢，可能造成控制不及时，使得稳定裕度下降。

2.1 理想 PI 控制器

\begin{aligned} Δ y & = K_{P} (ε + \frac{1}{T_{I}} \int_{0}^{t} ε d t) W (s) = K_{P} (1 + \frac{1}{T_{I} s}) \end{aligned}

积分时间 $T_{I}$ : 在阶跃信号作用下，积分作用的输出值变化等于比例作用的输出值所经历的时间。
积分时间越短，积分速度越快、积分作用越强。

2.2 实际 PI 控制器

\begin{array}{r} W (s) = K_{P} \frac{1 + \frac{1}{T_{I} s}}{1 + \frac{1}{K_{I} T_{I} s}} Δ y = K_{P} ε [1 + (K_{I} - 1) (1 - e^{- \frac{t}{K_{I} T_{I}}})] \end{array}

积分增益 $K_{I} = \frac{Δ y (\infty)}{Δ y (0)}$ 表示阶跃信号作用下，PI 控制器输出变化的最终值与比例输出值之比

控制点偏差： $ε_{m a x} = \frac{y_{m a x} - y_{m i n}}{K_{P} K_{I}}$ PI 控制器不可能完全消除余差
控制精度: $Δ = \frac{ε_{m a x}}{x_{m a x} - x_{m i n}} \times 100 % = \frac{1}{K_{P} K_{I}} \times 100 %$ 控制点最大偏差的相对变化值

控制精度表征消除余差的能力， $K_{I}$ 或 $K_{I} K_{P}$ 越大，控制精度越高，消除余差的能力越大。
不能完全消除余差：因为积分增益为有限值。

三、PD 运算规律

微分作用按偏差变化速度进行控制，只要有变化趋势，就有控制作用输出。
超前控制，可以改善控制过程的动态特性。噪声过大的系统不宜单独使用。

3.1 理想 PD 控制器

\begin{array}{r} Δ y = K_{P} (ε + T_{D} \frac{d ε}{d t}) W (s) = K_{P} (s) (1 + T_{D} s) \end{array}

微分时间 $T_{D}$ ：达到相同的输出值 $Δ y$ 时，微分作用比比例作用提前的时间。
微分时间越长，微分作用越强。（过大可能引起高频振荡）

3.2 实际 PD 控制器

\begin{array}{r} W (s) = K_{P} (s) \frac{1 + T_{D} s}{1 + \frac{T_{D}}{K_{D}} s} Δ y = K_{P} ε [1 + (K_{D} - 1) e^{- \frac{K_{D}}{T_{D}} t}] \end{array}

微分增益： $K_{D} = \frac{Δ y (0)}{Δ y (\infty)}$ 阶跃信号作用下，PD 控制器输出变化的初始值与最终值的比。
微分增益越大，微分作用越理想。
（阶跃信号作用下，实际 PD 控制器的输出从最大值下降到微分输出幅度的 36.8%所经历的时间为微分时间常数 $\frac{T_{D}}{K_{D}}$ ，再乘以微分增益，就得到微分时间）

四、PID 运算规律

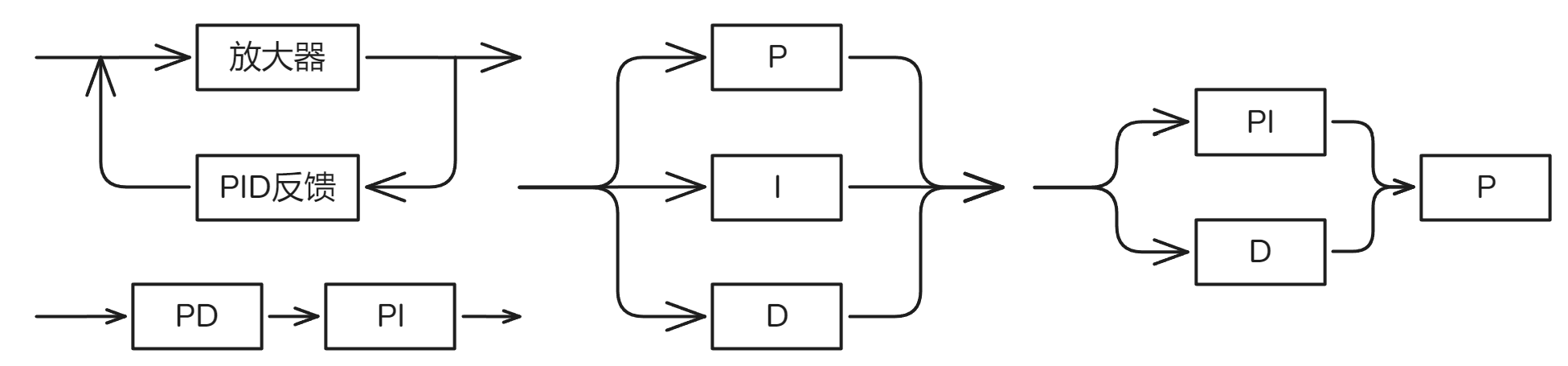
PID 控制器的构成

放大器和 PID 反馈电路：运算电路简单，相互干扰系数大
PD 和 PI 电路串联：相互干扰系数较小，各级串联使得累计误差较大，精度要求较高
P、I、D 电路并联：避免级间误差累计增大，实际参数发生改变
PI 与 D 并联后再与 P 串联：避免级间误差累计增大，不存在变量相互影响

注意明确调节 PID参数时，参数的实际意义
比例/积分/微分增益还是比例度、积分时间、微分时间