离散系统的稳定性分析

Stability Analysis of Discrete Systems

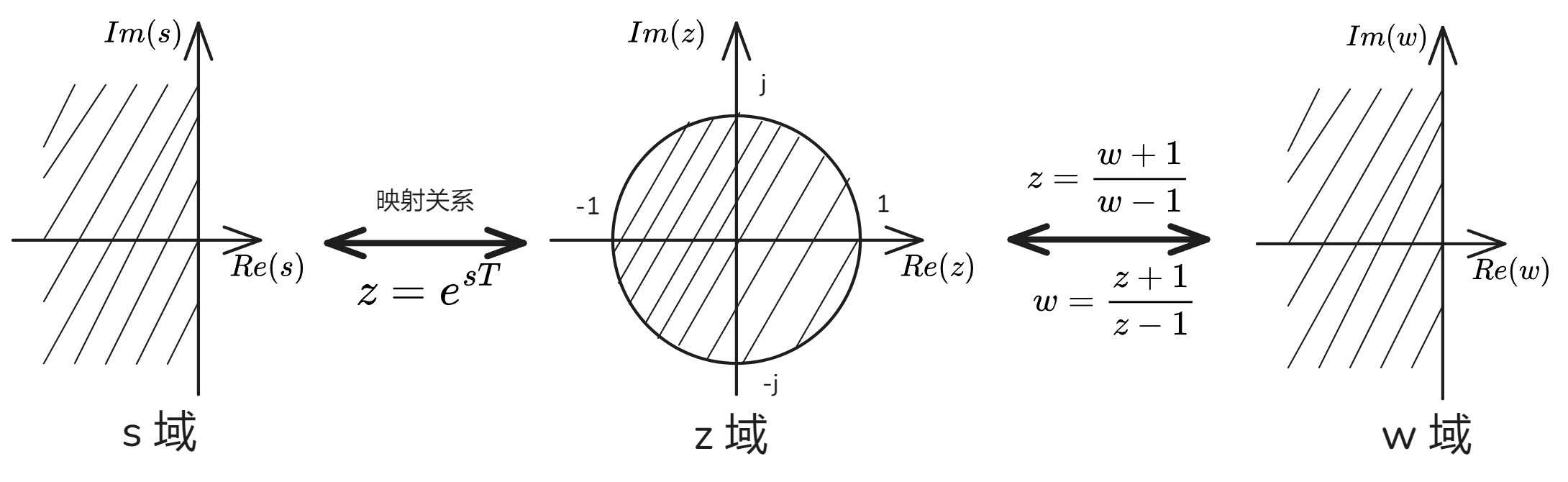
由线性系统稳定性分析知道：线性连续系统的闭环传递函数的极点都在 s 域的左半平面时，系统稳定。类似的，由映射关系可以得到，离散系统稳定的充分必要条件为：系统的闭环 z 传递函数的所有极点都在 z 平面的单位圆内部， $| p_{i} | < 1$

\begin{array}{r} s = σ + j ω \Rightarrow z = e^{s T} = e^{σ T} e^{j ω T} {\begin{cases} r_{z} = e^{σ T} \\ θ = ω T \end{cases} \end{array}

连续系统中：线性系统稳定性分析#2. 劳斯判据
引入与 z 变换为双线性变换的 w 变换，将单位圆映射到 w 平面的左半平面

\begin{array}{r} z = \frac{w + 1}{w - 1} \Leftrightarrow w = \frac{z + 1}{z - 1} \end{array}

对闭环传递函数的特征方程进行 w 变换，得到 w 特征方程：

W (s) = a_{n} w^{n} + a_{n - 1} w^{n - 1} + \dots + a_{1} w + a_{0} = 0

离散系统稳定的充分必要条件为：第一列各值均为正值

$w^{n}$	$a_{n}$	$a_{n - 2}$	$a_{n - 4}$	$\dots$
$w^{n - 1}$	$a_{n - 1}$	$a_{n - 3}$	$a_{n - 5}$	$\dots$
$w^{n - 2}$	$L_{31}$	$L_{32}$	$L_{33}$	$\dots$
$w^{n - 3}$	$L_{41}$	$L_{42}$	$L_{43}$	$\dots$
$\dots$	$\dots$	$\dots$	$\dots$	$\dots$
$w^{0}$	$\dots$

\begin{array}{r} L_{31} = - \frac{1}{a_{n - 1}} | \begin{array}{c} a_{n} & a_{n - 2} \\ a_{n - 1} & a_{n - 3} \end{array} | \\ L_{32} = - \frac{1}{a_{n - 1}} | \begin{array}{c} a_{n} & a_{n - 4} \\ a_{n - 1} & a_{n - 5} \end{array} | \\ L_{33} = - \frac{1}{a_{n - 1}} | \begin{array}{c} a_{n} & a_{n - 6} \\ a_{n - 1} & a_{n - 7} \end{array} | \\ L_{41} = - \frac{1}{L_{31}} | \begin{array}{c} a_{n - 1} & a_{n - 3} \\ L_{31} & L_{32} \end{array} | \\ L_{42} = - \frac{1}{L_{31}} | \begin{array}{c} a_{n - 1} & a_{n - 5} \\ L_{31} & L_{33} \end{array} | \end{array}

直接在 z 域根据线性离散系统的闭环特征方程进行稳定性判别

\begin{array}{r} α (z) = a_{0} z^{n} + a_{1} z^{n - 1} + \dots + a_{n} = 0 \end{array}

离散系统稳定的充分必要条件为：所有奇数行第一列元素均大于零（ $a_{0}, b_{0}, \dots, m_{0} > 0$ ），即特征方程的全部特征根均在单位圆内。
如果有小于零的元素，则离散系统不稳定，且小于零的元素个数就是位于圆外的特征根的个数。

	$z^{n}$	$z^{n - 1}$	$z^{n - 2}$	$\dots$	$z^{2}$	$z^{1}$	$z^{0}$
✅	$a_{0}$	$a_{1}$	$a_{2}$	$\dots$	$a_{n - 2}$	$a_{n - 1}$	$a_{n}$
	$a_{n}$	$a_{n - 1}$	$a_{n - 2}$	$\dots$	$a_{2}$	$a_{1}$	$a_{0}$
✅	$b_{0}$	$b_{1}$	$b_{2}$	$\dots$	$b_{n - 2}$	$b_{n - 1}$
	$b_{n - 1}$	$b_{n - 2}$	$b_{n - 3}$	$\dots$	$b_{2}$	$b_{0}$
✅	$c_{0}$	$c_{1}$	$c_{2}$	$\dots$	$c_{n - 2}$
	$c_{n - 2}$	$c_{n - 3}$	$c_{n - 4}$	$\dots$	$c_{0}$
	$⋮$	$⋮$	$⋮$
✅	$l_{0}$	$l_{1}$
	$l_{1}$	$l_{0}$
✅	$m_{0}$

\begin{array}{r} b_{0} = a_{0} - a_{n} \frac{a_{n}}{a_{0}} b_{1} = a_{1} - a_{n - 1} \frac{a_{n}}{a_{0}} b_{2} = a_{2} - a_{n - 2} \frac{a_{n}}{a_{0}} \dots \\ c_{0} = b_{0} - b_{n - 1} \frac{b_{n - 1}}{b_{0}} c_{1} = b_{1} - b_{n - 2} \frac{b_{n - 1}}{b_{0}} c_{2} = b_{2} - b_{n - 3} \frac{b_{n - 1}}{b_{0}} \dots \end{array}