Discretization of Analog Controllers
离散系统控制设计完后,都写上控制器算法
一、响应不变法(z 变换法)
1.1 脉冲响应不变法
基本思想:数字控制器 产生的脉冲响应序列与模拟控制器 产生的脉冲响应序列在采样瞬间相等。由于 ,实际上就是对 取 z 变换:
如果原控制器稳定,则离散化后也稳定
不具有串联性质
1.2 阶跃响应不变法
基本思想:数字控制器 产生的单位阶跃响应与模拟控制器 产生的单位阶跃响应在采样瞬间相等。实际上就是 ZOH 串联的广义对象 的 z 变换:
如果原控制器稳定,则离散化后也稳定
不具有串联性质
例子: ,求阶跃响应不变法对应的数字控制器,以及对应的差分方程
进一步得到差分方程:
二、差分变换法
将微分方程中的导数项用有限差分来近似等效,得到一个与原微分方程逼近的差分方程。欧拉法
根据 z 变换 的定义,以及泰勒级数展开有:
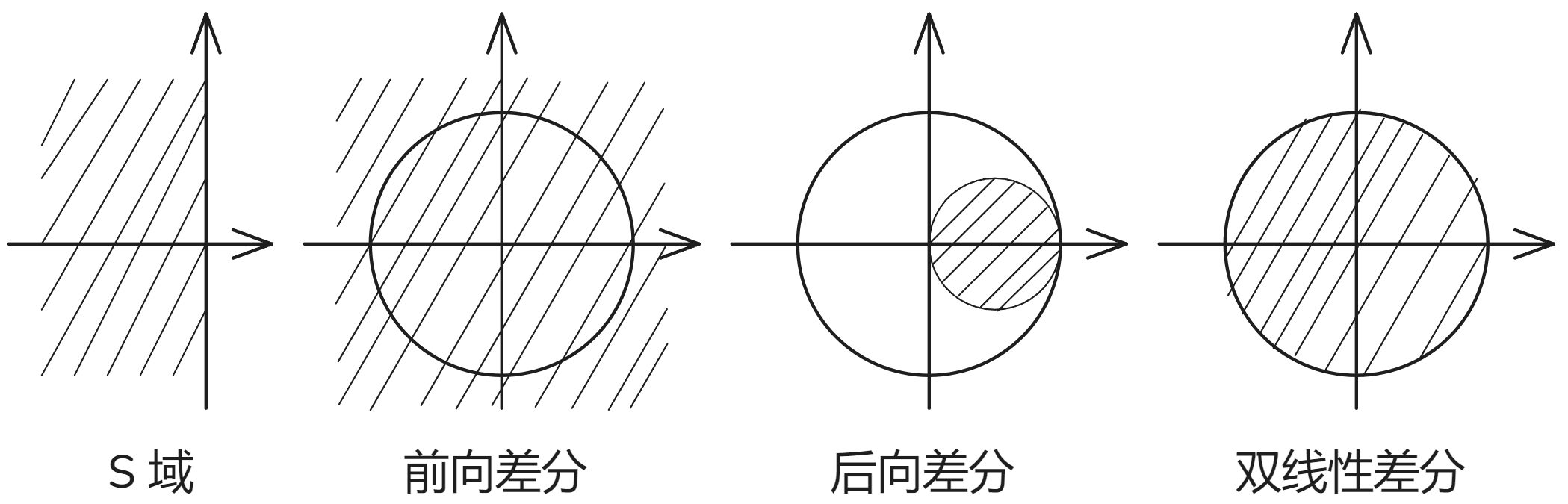
离散化稳态增益保持不变,都不能保持脉冲响应和频率响应
1. 前向差分
前向差分可能将 s 域左半平面的稳定极点映射到 z 平面单位圆外。
原控制器 稳定时,数字控制器 不一定稳定,实际一般不用前向差分
2. 后向差分
后向差分将 s 域左半平面的稳定极点映射到 z 平面单位圆内的一个小圆内。
如果 稳定,则离散化的数字控制器 也一定稳定。(应用较多)
(映射关系有畸变,变换精度较低)
3. 双线性差分 Tustin 变换法
双线性差分将 s 域左半平面的稳定极点映射到 z 平面单位圆内。
如果 稳定,则离散化的数字控制器 也一定稳定。(应用较多)
注意得到数字控制器后,如果要进一步得到差分方程,要注意不要出现 的项,可以上下同除以
三、零极点匹配法
基本步骤:
- 将模拟控制器写为零极点的形式,
- 将零点或极点按照 映射到 z 平面:
- 当极点数为 ,零点数为 时,在分母上补充 ,保证零极点个数相等
- 选定经典输入信号,按照稳态增益相等的原则匹配增益
模拟控制器使用:拉普拉斯变换#6.极限性质 数字控制器使用: z 变换#4. 极限定理
经典控制输入信号的选择要保证:原来的模拟控制器稳态为常数,才有意义
注意写为零极点形式(无论是模拟控制器还是数字控制器),都要在形式上把增益分离出来,避免混淆
