数字控制器

Digital Controller

一、基本思想

将系统中被控对象及零阶保持器进行离散化，得到广义对象 $G (z) = Z [G_{h} (s) G_{0} (s)]$
根据系统的性能指标及约束条件，确定闭环期望传递函数 $Φ (z)$ 或误差传递函数 $Φ_{e} (z)$
进一步得到数字控制器 $D (z)$
将 $D (z)$ 写为差分方程的形式，得到控制算法

二、数字控制器一般形式

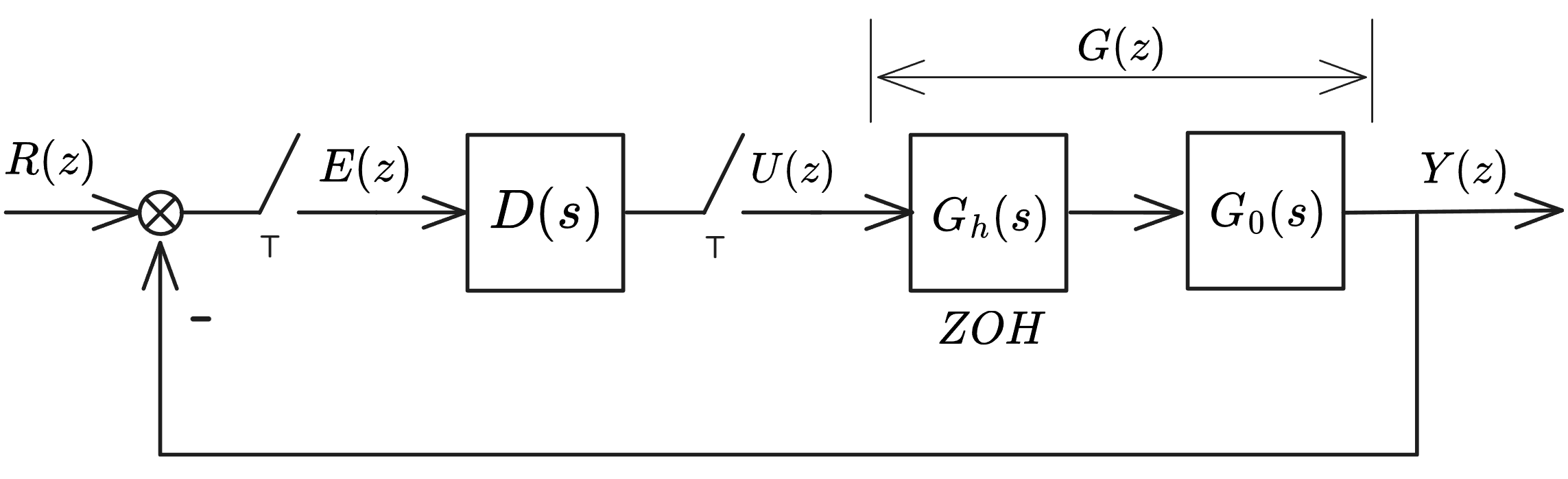
广义对象传递函数：

\begin{array}{r} G (z) = Z [G_{h} (s) G_{0} (s)] = G_{h} G_{0} (z) = (1 - z^{- 1}) Z [\frac{G_{0} (s)}{s}] \end{array}

误差传递函数及误差序列：

\begin{array}{r} Φ_{e} (z) = \frac{E (z)}{R (z)} = \frac{1}{1 + D (z) G (z)} e (k) = Z^{- 1} [Φ_{e} (z) R (z)] \end{array}

闭环传递函数及输出序列：

\begin{array}{r} Φ (z) = \frac{Y (z)}{R (z)} = \frac{D (z) G (z)}{1 + D (z) G (z)} = 1 - Φ_{e} (z) y (k) = Z^{- 1} [Φ (z) R (z)] \end{array}

\begin{array}{r} Y (z) + E (z) = R (z) y (k) = r (k) - e (k) \end{array}

数字控制器及控制序列：

\begin{array}{r} D (z) = \frac{U (z)}{E (z)} = \frac{1}{G (z)} \frac{Φ (z)}{1 - Φ (z)} u (k) = Z^{- 1} [D (z) E (z)] \end{array}

Question

离散序列指的是 $u (k T)$ ，为书写方便，可以直接写为 $u (k)$

零阶保持器和惯性环节串联的 z 变换

Important

由于出现的频率十分高，甚至可以作为结论来简化计算量！

计算反复出现错误

符号
漏乘 $(1 - z^{- 1})$ ，非常容易漏项！！！注意次数要相等
$e^{- T / T_{1}} \cdot e^{- T / T_{2}} = e^{- T (1 / T_{1} + 1 / T_{2})}$ 幂次相加，而不是 $e^{T^{2} / (T_{1} T_{2})}$
千万注意公式的记忆！！！注意是和零阶保持器相乘得到的结果
注意次数！！！注意 $z^{- 1}$
公式都是不带放大倍速的，实际做题要乘以系数！

1. 零阶保持器和一阶惯性环节串联 (一阶)

\begin{aligned} Z [\frac{1 - e^{- s T}}{s} \times \frac{1}{T_{1} s + 1}] \\ = & (1 - z^{- 1}) Z [\frac{1}{s (T_{1} s + 1)}] = (1 - z^{- 1}) Z [\frac{1}{s} - \frac{T_{1}}{T_{1} s + 1}] \\ = & (1 - z^{- 1}) Z [\frac{1}{s} - \frac{1}{s + \frac{1}{T_{1}}}] = (1 - \frac{1 - z^{- 1}}{1 - e^{- T / T_{1}} z^{- 1}}) \\ = & \frac{(1 - e^{- T / T_{1}}) z^{- 1}}{1 - e^{- T / T_{1}} z^{- 1}} \end{aligned}

2. 零阶保持器和一阶惯性环节与一阶积分串联 (二阶)

\begin{aligned} Z [\frac{1 - e^{- s T}}{s} \times \frac{1}{s (T_{1} s + 1)}] = (1 - z^{- 1}) Z [\frac{1}{s^{2} (T_{1} s + 1)}] \\ = & (1 - z^{- 1}) Z [\frac{1}{s^{2}} + \frac{- T_{1}}{s} + \frac{T_{1}}{s + \frac{1}{T_{1}}}] \\ = & \frac{T z^{- 1} - T_{1} (1 - z^{- 1})}{1 - z^{- 1}} + \frac{T_{1} (1 - z^{- 1})}{1 - e^{- T / T_{1}} z^{- 1}} \\ = & \frac{(T - T_{1} + T_{1} e^{- T / T_{1}}) z^{- 1} + (T_{1} - T e^{- T / T_{1}} - T_{1} e^{- T / T_{1}}) z^{- 2}}{(1 - z^{- 1}) (1 - e^{- T / T_{1}} z^{- 1})} \\ = & \frac{c_{1} z^{- 1} + c_{2} z^{- 2}}{(1 - z^{- 1}) (1 - e^{- T / T_{1}} z^{- 1})} \\ {\begin{cases} c_{1} = T - T_{1} + T_{1} e^{- T / T_{1}} \\ c_{2} = T_{1} - (T + T_{1}) e^{- T / T_{1}} \end{cases} \end{aligned}

3. 零阶保持器和二阶惯性环节串联（二阶）

\begin{aligned} Z [\frac{1 - e^{- T s}}{s} \frac{1}{(T_{1} s + 1) (T_{2} s + 1)}] = (1 - z^{- 1}) Z [\frac{1}{s} + \frac{- \frac{T_{1}}{T_{1} - T_{2}}}{s + \frac{1}{T_{1}}} + \frac{- \frac{T_{2}}{T_{2} - T_{1}}}{s + \frac{1}{T_{2}}}] \\ = & (1 - z^{- 1}) [\frac{1}{1 - z^{- 1}} + \frac{- \frac{T_{1}}{T_{1} - T_{2}}}{1 - e^{- T / T_{1}} z^{- 1}} + \frac{- \frac{T_{2}}{T_{2} - T_{1}}}{1 - e^{- T / T_{2}} z^{- 1}}] \\ = & \frac{(1 - (e^{- T / T_{1}} + e^{- T / T_{2}}) z^{- 1} + e^{(- T / T_{1}) - (T / T_{2})} z^{2}) + (1 - z^{- 1}) (- 1 + \frac{T_{1}}{T_{1} - T_{2}} e^{- T / T_{2}} z^{- 1} + \frac{T_{2}}{T_{2} - T_{1}} e^{- T / T_{1}} z^{- 1})}{(1 - e^{- T / T_{1}} z^{- 1}) (1 - e^{- T / T_{2}} z^{- 1})} \\ = & \frac{(1 - (e^{- T / T_{1}} + e^{- T / T_{2}}) z^{- 1} + e^{(- T / T_{1}) - (T / T_{2})} z^{2}) + - 1 + (1 + \frac{T_{1}}{T_{1} - T_{2}} e^{- T / T_{2}} + \frac{T_{2}}{T_{2} - T_{1}} e^{- T / T_{1}}) z^{- 1} + (\frac{T_{1}}{T_{2} - T_{1}} e^{- T / T_{2}} + \frac{T_{2}}{T_{1} - T_{2}} e^{- T / T_{1}}) z^{2}}{(1 - e^{- T / T_{1}} z^{- 1}) (1 - e^{- T / T_{2}} z^{- 1})} \\ = & \frac{(1 + \frac{T_{1}}{T_{1} - T_{2}} e^{- T / T_{2}} + \frac{T_{2}}{T_{2} - T_{1}} e^{- T / T_{1}} + e^{- T / T_{1}} + e^{- T / T_{2}}) z^{- 1} + (e^{(- T / T_{1}) - (T / T_{2})} + \frac{T_{1}}{T_{2} - T_{1}} e^{- T / T_{2}} + \frac{T_{2}}{T_{1} - T_{2}} e^{- T / T_{1}}) z^{2}}{(1 - e^{- T / T_{1}} z^{- 1}) (1 - e^{- T / T_{2}} z^{- 1})} \\ = & \frac{(c_{1} + c_{2} z^{- 1}) z^{- 1}}{(1 - e^{- T / T_{1}} z^{- 1}) (1 - e^{- T / T_{2}} z^{- 1})} \\ {\begin{cases} c_{1} = 1 + \frac{T_{2}}{T_{1} - T_{2}} e^{- T / T_{2}} + \frac{T_{1}}{T_{2} - T_{1}} e^{- T / T_{1}} = 1 + \frac{T_{1} e^{- T / T_{1}} - T_{2} e^{- T / T_{2}}}{T_{2} - T_{1}} \\ c_{2} = e^{- T (1 / T_{1} + 1 / T_{2})} + \frac{T_{1} e^{- T / T_{2}} - T_{2} e^{- T / T_{1}}}{T_{2} - T_{1}} \end{cases} \end{aligned}

数字控制器的可实现性

所谓控制器的可实现性，是指在控制算法中，不允许出现未来时刻的偏差值，即要求数字控制器 $G (z)$ 中不能有 $z$ 的正幂次项

常用数字控制器

参数优化的低阶算法
 数字 PID 控制器
 最小拍控制器
 大林算法控制器