Deadbeat Response 最少调节时间/暂态过程时间最少系统
在经典输入信号作用下,系统可经过最小拍使输出响应的稳态误差为零。(某种特定的输入在最少个采样周期内达到无静差的稳态) 实现时间最优控制
一、最小拍系统的具体要求
- 无静差:特定参考输入信号,在达到稳态后,在采样点的输出值准确跟随输入信号,不存在静差
- 最小拍:在有限拍内达到稳态,准确跟随输入信号所需的采样周期最少
- 可实现:必须在物理上可实现
- 稳定:闭环系统必须稳定
二、最小拍控制控制器的设计
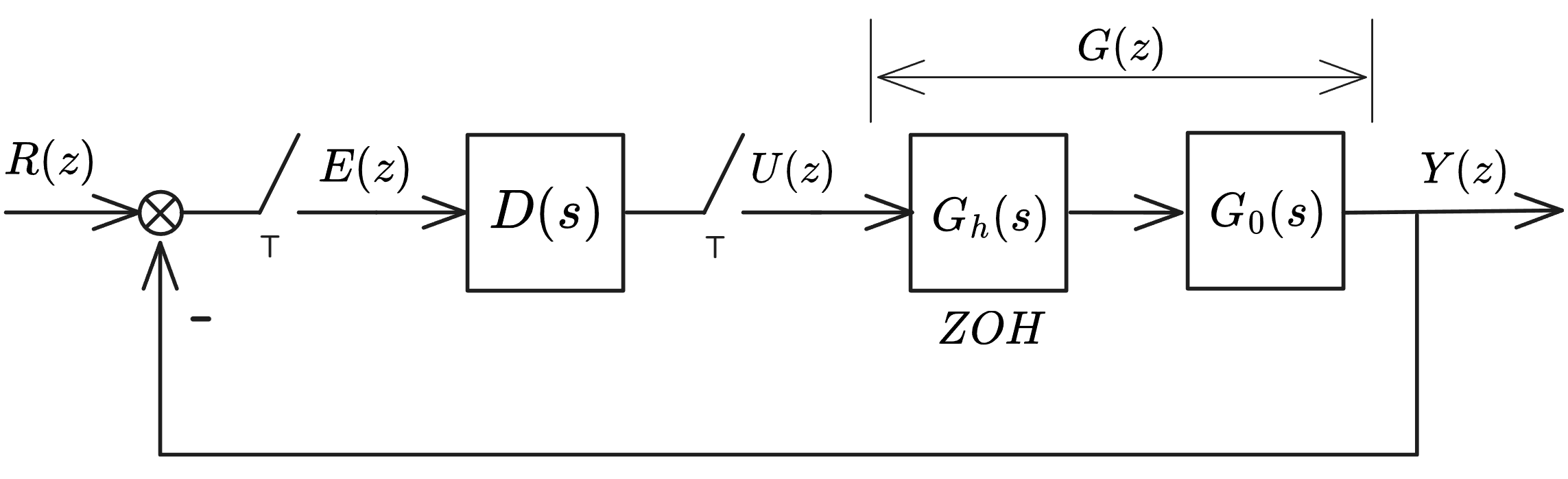
数字控制器
广义对象传递函数:
注意要写为标准型,便于观察是否存在单位圆外的零极点,例如:
1. 输入信号的类型(基础)
根据输入信号的类型,在误差传递函数上消除误差
输入信号的一般形式及稳态误差:
满足稳态误差为零且最小拍的误差传递函数:
得到期望的闭环传递函数:
进一步得到数字控制器:
| 输入信号 |
误差传递函数 |
闭环传递函数 |
| 单位阶跃 |
|
|
| 单位速度 |
|
|
| 单位加速度 |
|
|
2. 对象存在纯滞后
如果对象存在纯滞后,需要在闭环传递函数上将纯滞后消除
注意广义对象由于串联零阶保持器,带 一个纯滞后,这个纯滞后是不计算在对象的纯滞后上的。一般如果对象表示为 ,则表示有 个纯滞后
3. 对象存在单位圆外零点
对象单位圆外零点在闭环传递函数消除
4. 对象存在单位圆外极点
对象单位圆外极点在误差传递函数消除
5. 对象存在单位圆上极点 (1,0)
单位圆上极点 (1,0)个数为 k, 则 中 的最高次数只需要取输入的次数和单位圆上极点个数的最大值
三、全部情况综合以及实际例题
综合所有情况,保证 的最高次数相等
- 输入信号的类型
- 对象的纯延迟
- 单位圆外的零点
- 单位圆外的极点
- 单位圆上极点(1,0)
把 已知条件 放到前面
求出闭环传递函数时,不要急着拆开化简
零阶保持器的广义对象会带 ,不要看作为延迟, 看作 个延迟
注意计算:单位圆内外的判断!
在单位圆外
在单位圆内
四、最小拍控制器的局限性
- 不同输入信号适应性较差:最少拍控制器中的最少拍是针对某一典型输入设计的,对于其它典型输入则不一定为最少拍,甚至引起大的超调和静差
- 对参数变化过于敏感:如果系统参数发生变化,将使实际系统控制严重偏离期望状态
- 控制作用容易超过范围:设计时,对控制量未作限制
- 在采样点之间存在波纹(对象单位圆内零点):只能保证在采样点上的稳态误差为零,在许多情况下,系统在采样点之间的输出出现波纹,增加了执行机构的功率损耗和机械磨损
五、最小拍控制器的改进
最小拍控制器的改进
