点集
点
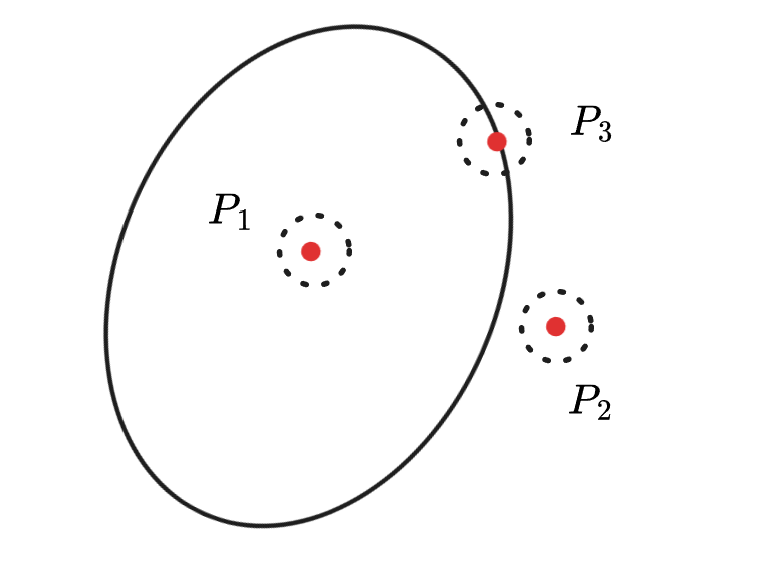
内点 Interior Point:
边界点 Boundary Point:
孤立点 Isolated Point:
集
开集 Open Set:
闭集 Closed Set:如果一个点集包含它的所有边界点,则该点集是闭集
余集:平面上不属于
有界集 Bounded Set:如果存在一个正数 𝛿 使得点集 𝐷完全包含在以原点为中心的 𝛿-邻域内,则 𝐷是有界集
无界集 Unbounded Set:如果点集不是有界集,则它是无界集
边界:边界点的全体
连通:平面点集
内点 Interior Point:
边界点 Boundary Point:
孤立点 Isolated Point:

开集 Open Set:
闭集 Closed Set:如果一个点集包含它的所有边界点,则该点集是闭集
余集:平面上不属于
有界集 Bounded Set:如果存在一个正数 𝛿 使得点集 𝐷完全包含在以原点为中心的 𝛿-邻域内,则 𝐷是有界集
无界集 Unbounded Set:如果点集不是有界集,则它是无界集
边界:边界点的全体
连通:平面点集