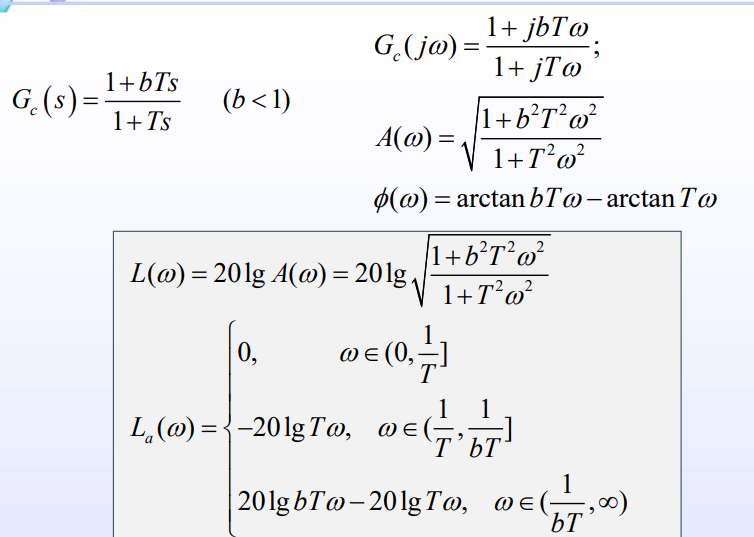适用于:
未校正系统的动态性能已经满足
但是稳定性能不满足要求
高频幅值衰减特性,使系统的截止频率减小
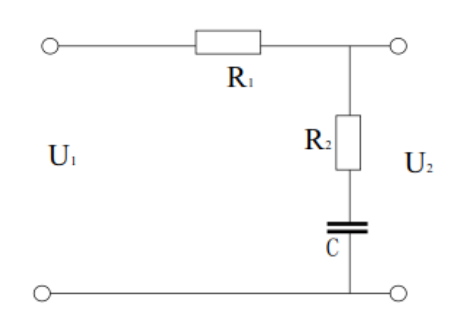
高频段的校正
利用滞后网络的高频幅值衰减特性,使系统的截止频率减小,获得足够的
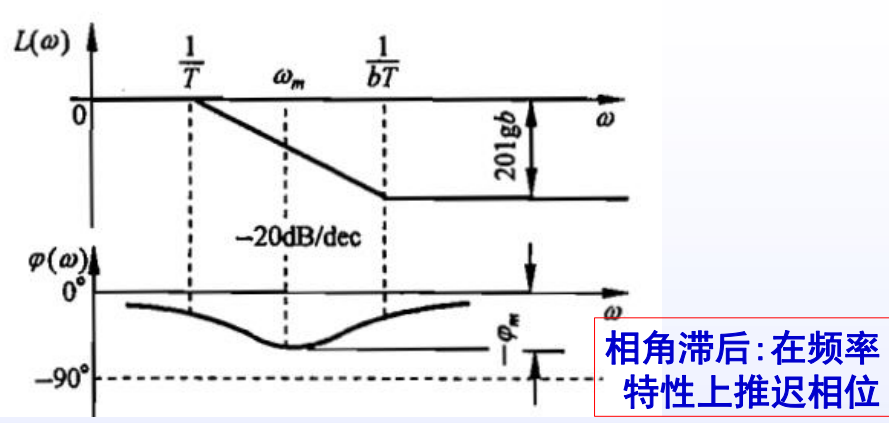
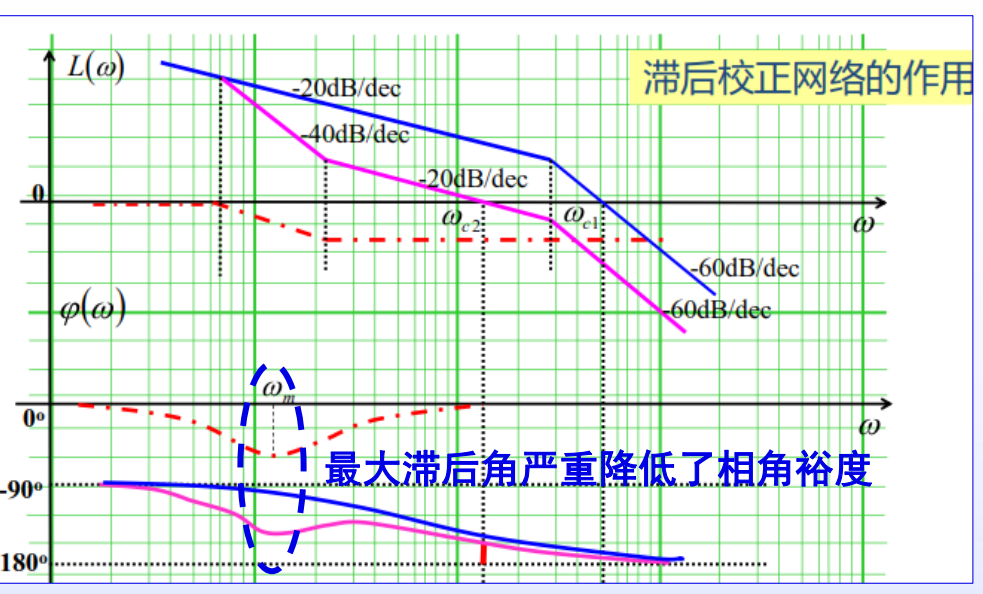
相关参数
分度系数:
时间常数:
转折频率:
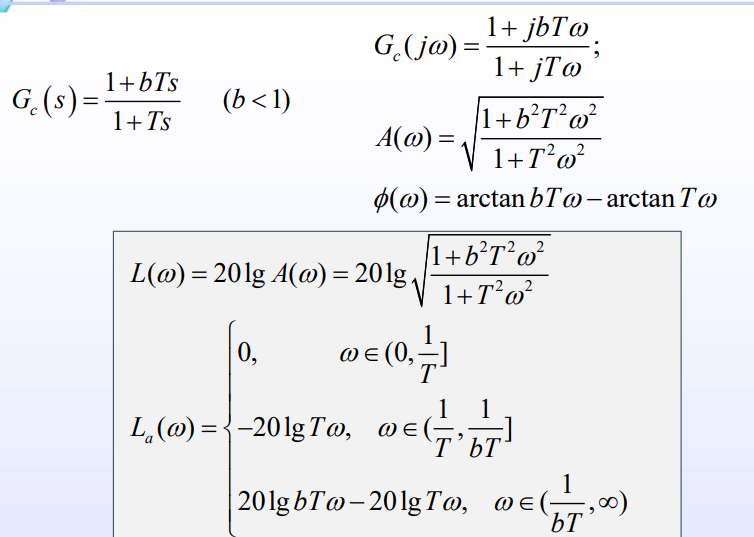
最大滞后角频率:
最大滞后角:
为了提高相角裕度,防止系统不稳定
选择滞后参数,使得第二个转折频率 (开环截止频率)
对系统的影响
- 降低中高频段幅值增益,提高了抗中高频干扰的能力
- 相角滞后,不利于相角裕度的提升(避免最大滞后角发生在已校正系统开环截止频率附近)
校正的设计步骤
-
根据稳态要求,确定未校正系统的放大系数
-
画出未校正系统 的 Bode 图 (渐近特性图)
求未校正系统的截止频率 与相角裕度
-
根据相位裕度 的要求,
确定未校正系统的相角裕度
取
以及校正后系统的截止频率
-
确定校正系数
利用滞后校正环节的高频段拉低未校正的曲线,降低截止频率,使得相角裕度符合要求
还要保证第二个转折频率远远小于新的截止频率
避免最大滞后角的影响
-
校正后的系统
校正环节