经典环节的传递函数

复杂传函的构成：基本环节
复杂传函的行为：由基本环节的行为决定

graph LR
经典环节 ----> 比例环节 & 积分环节 & 1[微分环节] & 二阶振荡环节 & 延迟环节

基本环节

1. 比例/放大环节

$G (s) = K$
$G (j ω) = K + j 0$

\begin{aligned} | G (j ω) | = K \\ L (ω) = 20 \lg K \\ ϕ (ω) = 0^{\circ} \end{aligned}

2. 纯积分环节

$G (s) = \frac{1}{s}$
$G (j ω) = \frac{1}{j ω} = 0 - j \frac{1}{ω}$

\begin{aligned} | G (j ω) | = \frac{1}{ω} \\ L (ω) = - 20 \lg ω \\ ϕ (ω) = - 90^{\circ} \end{aligned}

3. 纯微分环节

$G (s) = s$
$G (j ω) = j ω = 0 + j ω$

\begin{aligned} | G_{j ω} | = ω \\ L (ω) = 20 \lg ω \\ ϕ (ω) = 90^{\circ} \end{aligned}

4. 一阶惯性环节

$G (s) = \frac{1}{T s + 1}$
$G (j ω) = \frac{1}{1 + j ω T} = \frac{1}{1 + T^{2} ω^{2}} - j \frac{ω T}{1 + T^{2} ω^{2}}$

\begin{aligned} | G (j ω) | & = \frac{1}{\sqrt{1 + ω^{2} T^{2}}} \\ L (ω) & = 20 \lg | G (j ω) | \\ = - 10 \lg (1 + ω^{2} T^{2}) \\ \approx 0 (ω ≪ \frac{1}{T} 低 频 渐 近 线) \\ \approx - 20 \lg ω + 20 \lg \frac{1}{T} (ω ≫ \frac{1}{T} 高 频 特 性) \\ ϕ (ω) & = - \arctan ω T (0^{\circ}, - 90^{\circ}) \end{aligned}

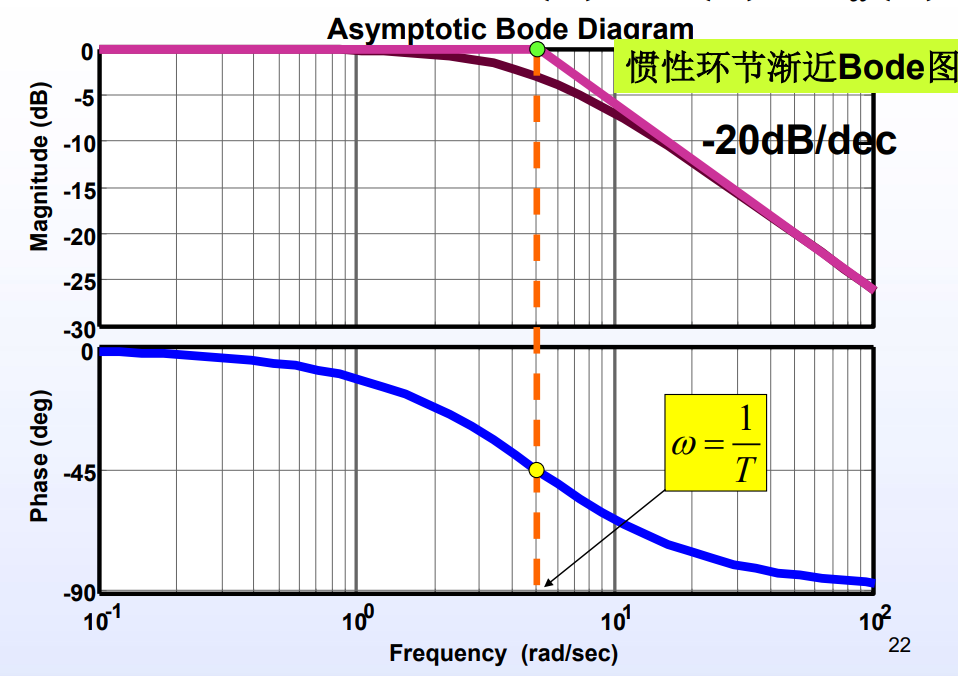
转折频率/交接频率： $ω = \frac{1}{T}$

对数幅频特性：曲线斜率为 $- 20 d B / d e c$ 渐近线
对数相频特性：对应 $- 45^{\circ}$ 转折点

带宽频率： $ω_{b} = \frac{1}{T}$
单位阶跃响应速度成正比

5. 一阶微分环节

$G (s) = τ s + 1$
$G (j ω) = 1 + j ω τ$

\begin{aligned} | G (j ω) | & = \sqrt{1 + ω^{2} τ^{2}} \\ L (ω) & = 20 \lg | G (j ω) | \\ = 10 \lg (1 + ω^{2} τ^{2}) \\ \approx 20 \lg (ω) - 20 l g (\frac{1}{τ}) (ω ≫ \frac{1}{τ} 高 频 特 性) \\ ϕ (ω) & = \arctan (ω τ) (0^{\circ}, 90^{\circ}) \end{aligned}

转折频率/交接频率 $ω = \frac{1}{τ}$

对数幅频特性：曲线斜率为 $20 d B / d e c$ 渐近线
对数相频特性：对应 $45^{\circ}$ 转折点

6. 二阶振荡环节

二阶系统

$G (s) = \frac{1}{T^{2} s^{2} + 2 T ζ s + 1} = \frac{1}{(\frac{s}{ω_{n}})^{2} + 2 ζ (\frac{s}{ω_{n}}) + 1}$
$G (j ω) = \frac{1}{1 - \frac{ω^{2}}{ω_{n}^{2}} + \frac{2 ζ ω}{ω_{n}} j}$

\begin{aligned} | G (j ω) | & = \frac{1}{\sqrt{{(1 - \frac{ω^{2}}{ω_{n}^{2}})}^{2} + 4 ζ^{2} \frac{ω^{2}}{ω_{n}^{2}}}} \\ L (ω) & = - 20 \lg \sqrt{{(1 - \frac{ω^{2}}{ω_{n}^{2}})}^{2} + 4 ζ^{2} \frac{ω^{2}}{ω_{n}^{2}}} \\ \approx 0 (ω ≪ ω_{n} 低 频 渐 近) \\ \approx - 40 \lg \frac{ω}{ω_{n}} (ω ≫ ω_{n} 高 频 渐 近) \end{aligned}

ϕ (ω) = {\begin{cases} - \arctan \frac{\frac{2 ζ ω}{ω_{n}}}{1 - \frac{ω^{2}}{ω_{n^{2}}}} ω \leq ω_{n} \\ - 180^{\circ} + \arctan \frac{\frac{2 ζ ω}{ω_{n}}}{\frac{ω^{2}}{ω_{n^{2}}} - 1} ω > ω_{n} \end{cases} (0^{\circ}, - 180^{\circ})

转折频率/交接频率: $ω = ω_{n}$

对数幅频特性：
- 低频特性：斜率为 $0 d B / d e c$ 渐近线
- 高频特性：斜率为 $- 40 d B / d e c$ 渐近线
对数相频特性：
对应 $- 90^{\circ}$ 转折点

谐振频率:
$ω_{r} = ω_{n} \sqrt{1 - 2 ζ^{2}} 0 < ζ < \frac{\sqrt{2}}{2} \approx 0.707$

谐振峰值:
最大幅值 $\frac{1}{2 ζ \sqrt{1 - ζ^{2}}}$
阻尼比越小，峰值越大

$ζ = 0$ 幅频特性曲线不连续，会产生分支
二阶系统的时域分析

7. 二阶微分环节

$G (s) = τ^{2} s^{2} + 2 ξ τ s + 1$
$G (j ω) = (1 - τ^{2} ω^{2}) + 2 ζ τ ω j$

\begin{aligned} | G (j ω) | & = \sqrt{(1 - τ^{2} ω^{2})^{2} + 4 ζ^{2} τ^{2} ω^{2}} \\ L (ω) & = 20 \lg \sqrt{(1 - τ^{2} ω^{2})^{2} + 4 ζ^{2} τ^{2} ω^{2}} \\ \approx 40 \lg ω τ (ω ≫ \frac{1}{τ} 高 频 渐 近) \end{aligned}

ϕ (ω) = {\begin{cases} \arctan \frac{\frac{2 ζ ω}{ω_{n}}}{1 - \frac{ω^{2}}{ω_{n^{2}}}} ω \leq ω_{n} \\ 180^{\circ} - \arctan \frac{\frac{2 ζ ω}{ω_{n}}}{\frac{ω^{2}}{ω_{n^{2}}} - 1} ω > ω_{n} \end{cases} (0^{\circ}, 180^{\circ})

转折频率/交接频率 $ω = ω_{n} = \frac{1}{τ}$

对数幅频特性：
- 低频特性：斜率为 $0 d B / d e c$ 渐近线
- 高频特性：斜率为 $40 d B / d e c$ 渐近线
对数幅频特性： $90^{\circ}$

9.延迟环节

输出量经恒定延时后，不失真地重复输入量变化的环节
$U_{o} (t) = U_{i} (t - τ)$
$G (s) = e^{- τ s} \approx \frac{1}{1 + τ s}$
$G (j ω) = e^{- j ω τ}$

\begin{aligned} | G (j ω) | & = 1 \\ L (ω) & = 0 \\ ϕ (ω) & = - ω τ \end{aligned}

非最小相位系统

对称关系

互为倒数的传递函数：
纯积分环节 --- 纯微分环节
一阶惯性环节 --- 一阶微分环节
二阶振荡环节 --- 二阶微分环节

Bode 图关于实轴对称

非最小相位系统和最小相位系统:

Nyquist 图
关于实轴对称
Bode 图
- 对数幅频特性曲线相同
- 对数相频特性曲线关于 0°线对称